2017年江苏省盐城市中考数学试卷
试卷更新日期:2017-07-03 类型:中考真卷
一、选择题:
-
1. ﹣2的绝对值是( )A、2 B、﹣2 C、 D、2. 如图是某个几何体的主视图、左视图、俯视图,该几何体是( )
 A、圆柱 B、球 C、圆锥 D、棱锥3. 下列图形中,是轴对称图形的是( )A、
A、圆柱 B、球 C、圆锥 D、棱锥3. 下列图形中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 数据6,5,7.5,8.6,7,6的众数是( )A、5 B、6 C、7 D、85. 下列运算中,正确的是( )A、7a+a=7a2 B、a2•a3=a6 C、a3÷a=a2 D、(ab)2=ab26. 如图,将函数y= (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
4. 数据6,5,7.5,8.6,7,6的众数是( )A、5 B、6 C、7 D、85. 下列运算中,正确的是( )A、7a+a=7a2 B、a2•a3=a6 C、a3÷a=a2 D、(ab)2=ab26. 如图,将函数y= (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )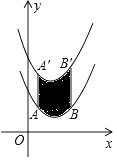 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
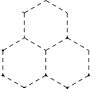
7. 请写出一个无理数 .8. 分解因式a2b﹣a的结果为 .9. 2016年12月30日,盐城市区内环高架快速路网二期工程全程全线通车,至此,已通车的内环高架快速路里程达57000米,用科学记数法表示数57000为 .10. 若 在实数范围内有意义,则x的取值范围是 .11. 如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是 .
 12. 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=°.
12. 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=°. 13. 若方程x2﹣4x+1=0的两根是x1 , x2 , 则x1(1+x2)+x2的值为 .14. 如图,将⊙O沿弦AB折叠,点C在 上,点D在 上,若∠ACB=70°,则∠ADB=°.
13. 若方程x2﹣4x+1=0的两根是x1 , x2 , 则x1(1+x2)+x2的值为 .14. 如图,将⊙O沿弦AB折叠,点C在 上,点D在 上,若∠ACB=70°,则∠ADB=°.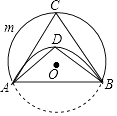 15.
15.如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为 .
 16.
16.如图,曲线l是由函数y= 在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4 ,4 ),B(2 ,2 )的直线与曲线l相交于点M、N,则△OMN的面积为 .

三、解答题
-
17. 计算: +( )﹣1﹣20170 .18. 解不等式组: .19. 先化简,再求值: ÷(x+2﹣ ),其中x=3+ .20. 为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
 (1)、小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是;(2)、小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.21. “大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
(1)、小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是;(2)、小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.21. “大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
请根据图中提供的信息,解答下列问题:
(1)、求被调查的学生总人数;(2)、补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;(3)、若该校共有800名学生,请估计“最想去景点B“的学生人数.22. 如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.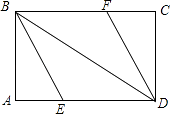 (1)、求证:四边形BEDF是平行四边形;(2)、当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.23. 某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.(1)、2014年这种礼盒的进价是多少元/盒?(2)、若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?24.
(1)、求证:四边形BEDF是平行四边形;(2)、当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.23. 某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.(1)、2014年这种礼盒的进价是多少元/盒?(2)、若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?24.如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
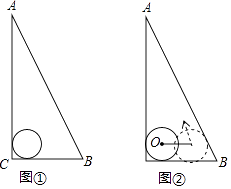 (1)、如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)(2)、如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.25. 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)、如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)(2)、如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.25. 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G. (1)、求证:BC是⊙F的切线;(2)、若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;(3)、试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.26.
(1)、求证:BC是⊙F的切线;(2)、若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;(3)、试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.26.综合题
 (1)、【探索发现】如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .(2)、【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 . (用含a,h的代数式表示)(3)、【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.(4)、【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC= ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.27.
(1)、【探索发现】如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .(2)、【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 . (用含a,h的代数式表示)(3)、【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.(4)、【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC= ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.27.如图,在平面直角坐标系中,直线y= x+2与x轴交于点A,与y轴交于点C,抛物线y= x2+bx+c经过A、C两点,与x轴的另一交点为点B.
 (1)、求抛物线的函数表达式;(2)、点D为直线AC上方抛物线上一动点;
(1)、求抛物线的函数表达式;(2)、点D为直线AC上方抛物线上一动点;①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1 , △BCE的面积为S2 , 求 的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.