2017年贵州省安顺市中考数学试卷
试卷更新日期:2017-07-03 类型:中考真卷
一、选择题
-
1. ﹣2017的绝对值是( )A、2017 B、﹣2017 C、±2017 D、﹣
-
2. 我国是世界上严重缺水的国家之一,目前我国每年可利用的淡水资源总量为27500亿米3 , 人均占有淡水量居全世界第110位,因此我们要节约用水,27500亿用科学记数法表示为( )A、275×104 B、2.75×104 C、2.75×1012 D、27.5×1011
-
3. 下了各式运算正确的是( )A、2(a﹣1)=2a﹣1 B、a2b﹣ab2=0 C、2a3﹣3a3=a3 D、a2+a2=2a2
-
4. 如图是一个圆柱体和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的俯视图为( )
 A、
A、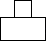 B、
B、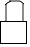 C、
C、 D、
D、
-
5. 如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
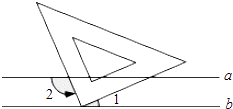 A、100° B、110° C、120° D、130°
A、100° B、110° C、120° D、130° -
6.
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
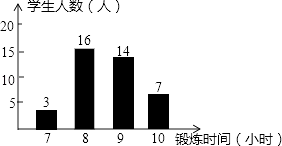 A、16,10.5 B、8,9 C、16,8.5 D、8,8.5
A、16,10.5 B、8,9 C、16,8.5 D、8,8.5 -
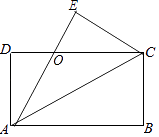
7. 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
 A、6cm B、7cm C、8cm D、9cm
A、6cm B、7cm C、8cm D、9cm -
8. 若关于x的方程x2+mx+1=0有两个不相等的实数根,则m的值可以是( )A、0 B、﹣1 C、2 D、﹣3
-
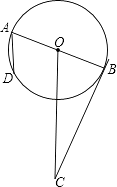
9. 如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 二次函数y=ax2+bx+c(≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠1),其中结论正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4
二、填空题
-
11. 分解因式:x3﹣9x= .
-
12. 在函数 中,自变量x的取值范围是 .
-
13. 三角形三边长分别为3,4,5,那么最长边上的中线长等于 .
-
14. 已知x+y= ,xy= ,则x2y+xy2的值为 .
-
15. 若代数式x2+kx+25是一个完全平方式,则k= .
-
16.
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为 cm.
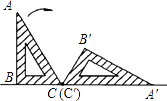
-
17.
如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 .

-
18.
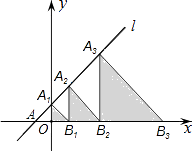
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1 , 点A2 , A3 , …在直线l上,点B1 , B2 , B3 , …在x轴的正半轴上,若△A1OB1 , △A2B1B2 , △A3B2B3 , …,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为 .
三、解答题
-
19. 计算:3tan30°+|2﹣ |+( )﹣1﹣(3﹣π)0﹣(﹣1)2017 .
-
20. 先化简,再求值:(x﹣1)÷( ﹣1),其中x为方程x2+3x+2=0的根.
-
21. 如图,DB∥AC,且DB= AC,E是AC的中点,
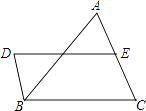 (1)、求证:BC=DE;(2)、连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?
(1)、求证:BC=DE;(2)、连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么? -
22. 已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
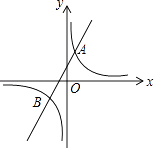 (1)、求这两个函数的表达式;(2)、根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
(1)、求这两个函数的表达式;(2)、根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围. -
23. 某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.(1)、求每件甲种、乙种玩具的进价分别是多少元?(2)、商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
-
24. 随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图,根据以下信息解答下列问题:
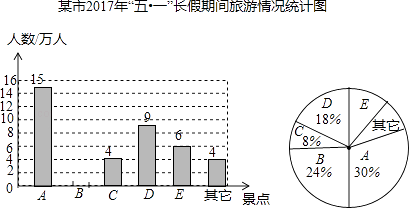 (1)、2017年“五•一”期间,该市周边景点共接待游客万人,扇形统计图中A景点所对应的圆心角的度数是 , 并补全条形统计图.(2)、根据近几年到该市旅游人数增长趋势,预计2018年“五•一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
(1)、2017年“五•一”期间,该市周边景点共接待游客万人,扇形统计图中A景点所对应的圆心角的度数是 , 并补全条形统计图.(2)、根据近几年到该市旅游人数增长趋势,预计2018年“五•一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果. -
25. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
 (1)、求证:BE与⊙O相切;(2)、设OE交⊙O于点F,若DF=1,BC=2 ,求阴影部分的面积.
(1)、求证:BE与⊙O相切;(2)、设OE交⊙O于点F,若DF=1,BC=2 ,求阴影部分的面积. -
26.
如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
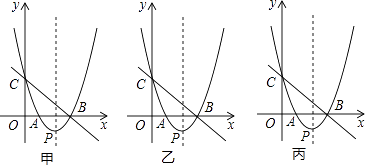 (1)、求该抛物线的解析式;(2)、在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;(3)、当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究).
(1)、求该抛物线的解析式;(2)、在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;(3)、当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究).
