2017年广东省中考数学试卷

试卷更新日期：2017-07-03 类型：中考真卷

进入出卷网下载

一、选择题

1. 5的相反数是（）

A、 $\frac{1}{5}$ B、5 C、﹣ $\frac{1}{5}$ D、﹣5

查看试题解析
2. “一带一路”倡议提出三年以来，广东企业到“一带一路”国家投资越来越活跃，据商务部门发布的数据显示，2016年广东省对沿线国家的实际投资额超过4000000000美元，将4000000000用科学记数法表示为（）

A、0.4×10⁹ B、0.4×10¹⁰ C、4×10⁹ D、4×10¹⁰

查看试题解析
3. 已知∠A=70°，则∠A的补角为（）

A、110° B、70° C、30° D、20°

查看试题解析
4. 如果2是方程x²﹣3x+k=0的一个根，则常数k的值为（）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析
5. 在学校举行“阳光少年，励志青春”的演讲比赛中，五位评委给选手小明的平分分别为：90，85，90，80，95，则这组数据的众数是（）

A、95 B、90 C、85 D、80

查看试题解析
6. 下列所述图形中，既是轴对称图形又是中心对称图形的是（）

A、等边三角形 B、平行四边形 C、正五边形 D、圆

查看试题解析
7. 如图，在同一平面直角坐标系中，直线y=k₁x（k₁≠0）与双曲线y= $\frac{k_{2}}{x}$ （k₂≠0）相交于A，B两点，已知点A的坐标为（1，2），则点B的坐标为（）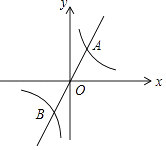

A、（﹣1，﹣2） B、（﹣2，﹣1） C、（﹣1，﹣1） D、（﹣2，﹣2）

查看试题解析
8. 下列运算正确的是（）

A、a+2a=3a² B、a³•a²=a⁵ C、（a⁴）²=a⁶ D、a⁴+a²=a⁴

查看试题解析
9. 如图，四边形ABCD内接于⊙O，DA=DC，∠CBE=50°，则∠DAC的大小为（）

A、130° B、100° C、65° D、50°

查看试题解析
10. 如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S_△_ABF=S_△_ADF；②S_△_CDF=4S_△_CEF；③S_△_ADF=2S_△_CEF；④S_△_ADF=2S_△_CDF ，其中正确的是（）

A、①③ B、②③ C、①④ D、②④

查看试题解析

二、填空题

11. 分解因式：a²+a= ．

查看试题解析
12. 一个n边形的内角和是720°，则n= ．

查看试题解析
13.
已知实数a，b在数轴上的对应点的位置如图所示，则a+b0．（填“＞”，“＜”或“=”）

查看试题解析
14. 在一个不透明的盒子中，有五个完全相同的小球，把它们分别标号为1，2，3，4，5，随机摸出一个小球，摸出的小球标号为偶数的概率是．

查看试题解析
15. 已知4a+3b=1，则整式8a+6b﹣3的值为．

查看试题解析
16. 如图，矩形纸片ABCD中，AB=5，BC=3，先按图（2）操作：将矩形纸片ABCD沿过点A的直线折叠，使点D落在边AB上的点E处，折痕为AF；再按图（3）操作，沿过点F的直线折叠，使点C落在EF上的点H处，折痕为FG，则A、H两点间的距离为．

查看试题解析

三、解答题

17. 计算：|﹣7|﹣（1﹣π）⁰+（ $\frac{1}{3}$ ）^﹣¹ ．

查看试题解析
18. 先化简，再求值：（ $\frac{1}{x - 2}$ + $\frac{1}{x + 2}$ ）•（x²﹣4），其中x= $\sqrt{5}$ ．

查看试题解析
19. 学校团委组织志愿者到图书馆整理一批新进的图书．若男生每人整理30本，女生每人整理20本，共能整理680本；若男生每人整理50本，女生每人整理40本，共能整理1240本．求男生、女生志愿者各有多少人？

查看试题解析
20. 如图，在△ABC中，∠A＞∠B．

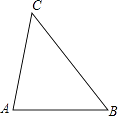(1)、作边AB的垂直平分线DE，与AB，BC分别相交于点D，E（用尺规作图，保留作图痕迹，不要求写作法）；

(2)、在（1）的条件下，连接AE，若∠B=50°，求∠AEC的度数．

查看试题解析
21. 如图所示，已知四边形ABCD，ADEF都是菱形，∠BAD=∠FAD，∠BAD为锐角．

(1)、求证：AD⊥BF；

(2)、若BF=BC，求∠ADC的度数．

查看试题解析
22. 某校为了解九年级学生的体重情况，随机抽取了九年级部分学生进行调查，将抽取学生的体重情况绘制如下不完整的统计图表，如图表所示，请根据图标信息回答下列问题：
体重频数分布表
组边
体重（千克）
人数
A
45≤x＜50
12
B
50≤x＜55
m
C
55≤x＜60
80
D
60≤x＜65
40
E
65≤x＜70
16

(1)、填空：①m=（直接写出结果）；
②在扇形统计图中，C组所在扇形的圆心角的度数等于度；

(2)、如果该校九年级有1000名学生，请估算九年级体重低于60千克的学生大约有多少人？

查看试题解析
23. 如图，在平面直角坐标系中，抛物线y=﹣x²+ax+b交x轴于A（1，0），B（3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C．

(1)、求抛物线y=﹣x²+ax+b的解析式；

(2)、当点P是线段BC的中点时，求点P的坐标；

(3)、在（2）的条件下，求sin∠OCB的值．

查看试题解析
24. 如图，AB是⊙O的直径，AB=4 $\sqrt{3}$ ，点E为线段OB上一点（不与O，B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，AF⊥PC于点F，连接CB．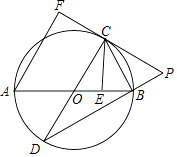

(1)、求证：CB是∠ECP的平分线；

(2)、求证：CF=CE；

(3)、当 $\frac{C F}{C P}$ = $\frac{3}{4}$ 时，求劣弧 $\hat{B C}$ 的长度（结果保留π）

查看试题解析
25.
如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2 $\sqrt{3}$ ，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．

(1)、填空：点B的坐标为；

(2)、是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；

(3)、①求证： $\frac{D E}{D B}$ = $\frac{\sqrt{3}}{3}$ ；
②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．

查看试题解析

组边	体重（千克）	人数
A	45≤x＜50	12
B	50≤x＜55	m
C	55≤x＜60	80
D	60≤x＜65	40
E	65≤x＜70	16