初中数学华师大版九年级上学期 第23章 23.3.4 相似三角形的应用
试卷更新日期：2019-10-16 类型：同步测试
一、单选题
-
1. 下列命题中，正确的个数是（ ）
①等边三角形都相似；②直角三角形都相似；③等腰三角形都相似；④锐角三角形都相似；⑤等腰三角形都全等；⑥有一个角相等的等腰三角形相似；⑦有一个钝角相等的两个等腰三角形相似；⑧全等三角形相似．
A、2个 B、3个 C、4个 D、5个2. 如图▱ABCD，F为BC中点，延长AD至E，使 ，连结EF交DC于点G，则 ＝（ ）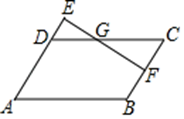
A、2：3 B、3：2 C、9：4 D、4：93. 学校门口的栏杆如图所示，栏杆从水平位置 绕 点旋转到 位置，已知 ， ，垂足分别为 ， ， ， ， ，则栏杆 端应下降的垂直距离 为（ ）
A、
B、
C、
D、
4. 如图，下列条件中不能判定△ACD∽△ABC的是（ ）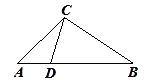
A、 B、∠ADC＝∠ACB C、∠ACD＝∠B D、AC2=AD·AB5. 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交DB于点F，则△DEF的面积与△BAF的面积之比为（ ）
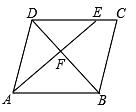A、1：3 B、3：4 C、1：9 D、9：166. 如图，小明在 时测得某树的影长为 ， 时又测得该树的影长为 ，若两次日照的光线互相垂直，则树的高度为（ ）m．
A、2 B、4 C、6 D、8二、填空题
-
7. 如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，测得落在地面上的影长BD=9.6米，留在墙上的影长CD=2米，则旗杆的高度AB为米.
8. 如图，A，B两点分别位于一个池塘的两端，为了测量A、B之间的距离，小天想了一个办法：在地上取一点C，使它可以直接到达A、B两点，连接AC，BC，在AC上取一点M，使AM=3MC，作MN//AB交BC于点N，测得MN=36m，则A、B两点间的距离为.
三、解答题
-
9. 如图，河对岸有一路灯杆AB，在灯光下，小亮在点D处测得自己的影长DF＝3m，沿BD方向从D后退4米到G处，测得自己的影长GH＝5，如果小亮的身高为1.7m，求路灯杆AB的高度.
10. 如图，一位测量人员要测量池塘的宽度AB的长，他过A、B两点画两条相交于点O的射线，在射线上取两点D、E，使 ，若测得DE=37.2米，他能求出A、B之间的距离吗?若能，请你帮他算出来：若不能，请你帮他设计一个可行方案。
11. 如图，在△ABC中，AB=4cm，BC=8cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，如果P、Q分别从A、B同时出发，经几秒后，点P、B、Q构成的三角形△PBQ与△ABC相似?
四、综合题
-
12. 如图，正方形ABCD的边长为2，E为AB的中点，P是BA延长线上的一点，连接PC交AD于点F，AP=FD
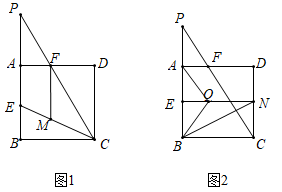(1)、求 的值(2)、如图1，连接EC，在线段EC上取一点M，使EM=EB，连接MF，求证MF=PF；(3)、如图2，过点E作EN⊥CD于点N，在线段EN上取一点Q，使AQ=AP，连接BQ，BN.将△AQB绕点A旋转，使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上，并说明理由.