初中数学华师大版九年级上学期 第23章 23.3.1 相似三角形

试卷更新日期：2019-10-16 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 若两个三角形的相似比为1:2，则它们的面积比为（ ）
    A、1:2 B、1:4 C、2:1 D、4:1

    查看试题解析

  • 2. 如图，在Rt△ABC内画有边长为9，6，x的三个正方形，则x的值为（   ）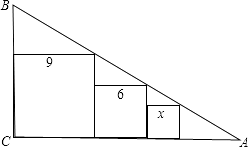

    A、3 B、4 C、3 5 D、5

    查看试题解析

  • 3. 相似三角形的概念是（   ）
    A、对应角相等、对应边成比例的两个三角形 B、两角分别相等的两个三角形 C、三边对应成比例的两个三角形 D、两边对应成比例且夹角相等的两个三角形

    查看试题解析

  • 4. 下列语句正确的是（　　）


    A、在△ABC和△A′B′C′中，∠B=∠B′=90°，∠A=30°，∠C′=60°，则△ABC和△A′B′C′不相似 B、△ABC和在△A′B′C′中，AB=5，BC=7，AC=8，A′C′=16，B′C′=14，A′B′=10，则△ABC∽△A′B′C′ C、两个全等三角形不一定相似 D、所有的菱形都相似

    查看试题解析

二、填空题

  • 5. 下列说法中：①所有的等腰三角形都相似；②所有的正三角形都相似；③所有的正方形都相似；④所有的矩形都相似．其中说法正确的序号是 ．

    查看试题解析

  • 6. 利用复印机的缩放功能，将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形，那么放大前后的两个三角形的周长比是 ．

    查看试题解析

三、综合题

  • 7.

    如图1．在菱形ABCD中，AB=2 5 ，tan∠ABC=2，∠BCD=α，点E从点D出发，以每秒1个单位长度的速度沿着射线DA的方向匀速运动，设运动时间为t（秒），将线段CE绕点C顺时针旋转α度，得到对应线段CF，连接BD、EF，BD交EC、EF于点P、Q．


    (1)、求证：△ECF∽△BCD；

    (2)、当t为何值时，△ECF≌△BCD？

    (3)、当t为何值时，△EPQ是直角三角形？

    查看试题解析

  • 8. 已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．且△OCP与△PDA的面积比为1：4

    (1)、

    如图1，已知折痕与边BC交于点O，连结AP、OP、OA．

    ①求证：△OCP∽△PDA；

    ②求边AB的长；

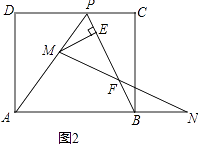
    (2)、

    如图2，连结AP、BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN=PM，连结MN交PB于点F，作ME⊥BP于点E．试问当点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，求出线段EF的长度．

    查看试题解析