2017年新疆生产建设兵团中考数学试卷
试卷更新日期:2017-07-03 类型:中考真卷
一、选择题
-
1. 下列四个数中,最小的数是( )A、﹣1 B、0 C、 D、32. 某几何体的三视图如图所示,则该几何体是( )
 A、球 B、圆柱 C、三棱锥 D、圆锥3. 已知分式 的值是零,那么x的值是( )A、﹣1 B、0 C、1 D、±14. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、通常温度降到0℃以下,纯净的水结冰 C、明天一定是晴天 D、经过有交通信号灯的路口,遇到红灯5. 下列运算正确的是( )A、6a﹣5a=1 B、(a2)3=a5 C、3a2+2a3=5a5 D、2a•3a2=6a36. 如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC等于( )
A、球 B、圆柱 C、三棱锥 D、圆锥3. 已知分式 的值是零,那么x的值是( )A、﹣1 B、0 C、1 D、±14. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、通常温度降到0℃以下,纯净的水结冰 C、明天一定是晴天 D、经过有交通信号灯的路口,遇到红灯5. 下列运算正确的是( )A、6a﹣5a=1 B、(a2)3=a5 C、3a2+2a3=5a5 D、2a•3a2=6a36. 如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC等于( )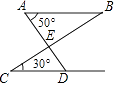 A、20° B、50° C、80° D、100°7. 已知关于x的方程x2+x﹣a=0的一个根为2,则另一个根是( )A、﹣3 B、﹣2 C、3 D、68. 某工厂现在平均每天比原计划多生产40台机器,现在生产600台机器所需的时间与原计划生产480台机器所用的时间相同,设原计划每天生产x台机器,根据题意,下面列出的方程正确的是( )A、 = B、 = C、 = D、 =9. 如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )
A、20° B、50° C、80° D、100°7. 已知关于x的方程x2+x﹣a=0的一个根为2,则另一个根是( )A、﹣3 B、﹣2 C、3 D、68. 某工厂现在平均每天比原计划多生产40台机器,现在生产600台机器所需的时间与原计划生产480台机器所用的时间相同,设原计划每天生产x台机器,根据题意,下面列出的方程正确的是( )A、 = B、 = C、 = D、 =9. 如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )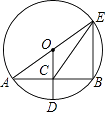 A、12 B、15 C、16 D、18
A、12 B、15 C、16 D、18二、填空题
-
10. 分解因式:x2﹣1= .11. 如图,它是反比例函数y= 图象的一支,根据图象可知常数m的取值范围是 .
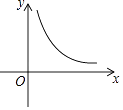 12. 某餐厅供应单位为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为元.
12. 某餐厅供应单位为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为元. 13. 一台空调标价2000元,若按6折销售仍可获利20%,则这台空调的进价是元.14. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 .
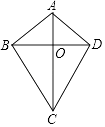
13. 一台空调标价2000元,若按6折销售仍可获利20%,则这台空调的进价是元.14. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 . 15. 如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
15. 如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S= AC•BD.
正确的是(填写所有正确结论的序号)
三、解答题(一)
-
16. 计算:( )﹣1﹣|﹣ |+ +(1﹣π)0 .17. 解不等式组 .18. 如图,点C是AB的中点,AD=CE,CD=BE.
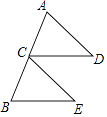 (1)、求证:△ACD≌△CBE;(2)、连接DE,求证:四边形CBED是平行四边形.19. 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)
(1)、求证:△ACD≌△CBE;(2)、连接DE,求证:四边形CBED是平行四边形.19. 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)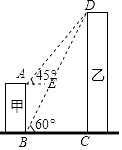
四、解答题(二)
-
20. 阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别
时间(小时)
频数(人数)
频率
A
0≤t≤0.5
6
0.15
B
0.5≤t≤1
a
0.3
C
1≤t≤1.5
10
0.25
D
1.5≤t≤2
8
b
E
2≤t≤2.5
4
0.1
合计
1
请根据图表中的信息,解答下列问题:
 (1)、表中的a= , b= , 中位数落在组,将频数分布直方图补全;(2)、估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?(3)、E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.21. 某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)、表中的a= , b= , 中位数落在组,将频数分布直方图补全;(2)、估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?(3)、E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.21. 某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.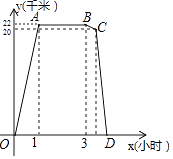 (1)、活动中心与小宇家相距千米,小宇在活动中心活动时间为小时,他从活动中心返家时,步行用了小时;(2)、求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);(3)、根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.22. 如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)、活动中心与小宇家相距千米,小宇在活动中心活动时间为小时,他从活动中心返家时,步行用了小时;(2)、求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);(3)、根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.22. 如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.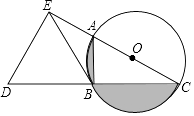 (1)、求证:BE是⊙O的切线;(2)、当BE=3时,求图中阴影部分的面积.23. 如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C.
(1)、求证:BE是⊙O的切线;(2)、当BE=3时,求图中阴影部分的面积.23. 如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C. (1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.
(1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)、在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.