2017年四川省眉山市中考数学试卷

试卷更新日期：2017-07-03 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列四个数中，比﹣3小的数是（）

A、0 B、1 C、﹣1 D、﹣5

查看试题解析
2. 不等式﹣2x＞ $\frac{1}{2}$ 的解集是（）

A、x＜﹣ $\frac{1}{4}$ B、x＜﹣1 C、x＞﹣ $\frac{1}{4}$ D、x＞﹣1

查看试题解析
3. 某微生物的直径为0.000 005 035m，用科学记数法表示该数为（）

A、5.035×10^﹣⁶ B、50.35×10^﹣⁵ C、5.035×10⁶ D、5.035×10^﹣⁵

查看试题解析
4. 如图所示的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列说法错误的是（）

A、给定一组数据，那么这组数据的平均数一定只有一个 B、给定一组数据，那么这组数据的中位数一定只有一个 C、给定一组数据，那么这组数据的众数一定只有一个 D、如果一组数据存在众数，那么该众数一定是这组数据中的某一个

查看试题解析
6. 下列运算结果正确的是（）

A、 $\sqrt{8}$ ﹣ $\sqrt{18}$ =﹣ $\sqrt{2}$ B、（﹣0.1）^﹣²=0.01 C、（ $\frac{2 a}{b}$ ）²÷ $\frac{b}{2 a}$ = $\frac{2 a}{b}$ D、（﹣m）³•m²=﹣m⁶

查看试题解析
7. 已知关于x，y的二元一次方程组 ${\begin{matrix} 2 a x + b y = 3 \\ a x - b y = 1 \end{matrix}$ 的解为 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ ，则a﹣2b的值是（）

A、﹣2 B、2 C、3 D、﹣3

查看试题解析
8. “今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为（）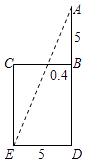

A、1.25尺 B、57.5尺 C、6.25尺 D、56.5尺

查看试题解析
9. 如图，在△ABC中，∠A=66°，点I是内心，则∠BIC的大小为（）

A、114° B、122° C、123° D、132°

查看试题解析
10. 如图，EF过▱ABCD对角线的交点O，交AD于E，交BC于F，若▱ABCD的周长为18，OE=1.5，则四边形EFCD的周长为（）

A、14 B、13 C、12 D、10

查看试题解析
11. 若一次函数y=（a+1）x+a的图象过第一、三、四象限，则二次函数y=ax²﹣ax（）

A、有最大值 $\frac{a}{4}$ B、有最大值﹣ $\frac{a}{4}$ C、有最小值 $\frac{a}{4}$ D、有最小值﹣ $\frac{a}{4}$

查看试题解析
12. 已知 $\frac{1}{4}$ m²+ $\frac{1}{4}$ n²=n﹣m﹣2，则 $\frac{1}{m}$ ﹣ $\frac{1}{n}$ 的值等于（）

A、1 B、0 C、﹣1 D、﹣ $\frac{1}{4}$

查看试题解析

二、填空题

13. 分解因式：2ax²﹣8a= ．

查看试题解析
14. △ABC是等边三角形，点O是三条高的交点．若△ABC以点O为旋转中心旋转后能与原来的图形重合，则△ABC旋转的最小角度是．

查看试题解析
15. 已知一元二次方程x²﹣3x﹣2=0的两个实数根为x₁ ， x₂ ，则（x₁﹣1）（x₂﹣1）的值是．

查看试题解析
16. 设点（﹣1，m）和点（ $\frac{1}{2}$ ，n）是直线y=（k²﹣1）x+b（0＜k＜1）上的两个点，则m、n的大小关系为．

查看试题解析
17. 如图，AB是⊙O的弦，半径OC⊥AB于点D，且AB=8cm，DC=2cm，则OC=cm．

查看试题解析
18. 已知反比例函数y= $\frac{2}{x}$ ，当x＜﹣1时，y的取值范围为．

查看试题解析

三、解答题：

19. 先化简，再求值：（a+3）²﹣2（3a+4），其中a=﹣2．

查看试题解析
20. 解方程： $\frac{1}{x - 2}$ +2= $\frac{1 - x}{2 - x}$ ．

查看试题解析
21.
在如图的正方形网格中，每一个小正方形的边长为1．格点三角形ABC（顶点是网格线交点的三角形）的顶点A、C的坐标分别是（﹣4，6），（﹣1，4）．

(1)、请在图中的网格平面内建立平面直角坐标系；

(2)、请画出△ABC关于x轴对称的△A₁B₁C₁；

(3)、请在y轴上求作一点P，使△PB₁C的周长最小，并写出点P的坐标．

查看试题解析
22.
如图，为了测得一棵树的高度AB，小明在D处用高为1m的测角仪CD，测得树顶A的仰角为45°，再向树方向前进10m，又测得树顶A的仰角为60°，求这棵树的高度AB．

查看试题解析
23. 一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球．若红球个数是黑球个数的2倍多40个．从袋中任取一个球是白球的概率是 $\frac{1}{29}$ ．

(1)、求袋中红球的个数；

(2)、求从袋中任取一个球是黑球的概率．

查看试题解析
24. 东坡某烘焙店生产的蛋糕礼盒分为六个档次，第一档次（即最低档次）的产品每天生产76件，每件利润10元．调查表明：生产提高一个档次的蛋糕产品，该产品每件利润增加2元．

(1)、若生产的某批次蛋糕每件利润为14元，此批次蛋糕属第几档次产品；

(2)、由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1080元，该烘焙店生产的是第几档次的产品？

查看试题解析
25. 如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交BC于G．

(1)、求证：BG=DE；

(2)、若点G为CD的中点，求 $\frac{H G}{G F}$ 的值．

查看试题解析
26.
如图，抛物线y=ax²+bx﹣2与x轴交于A、B两点，与y轴交于C点，已知A（3，0），且M（1，﹣ $\frac{8}{3}$ ）是抛物线上另一点．

(1)、求a、b的值；

(2)、连结AC，设点P是y轴上任一点，若以P、A、C三点为顶点的三角形是等腰三角形，求P点的坐标；

(3)、若点N是x轴正半轴上且在抛物线内的一动点（不与O、A重合），过点N作NH∥AC交抛物线的对称轴于H点．设ON=t，△ONH的面积为S，求S与t之间的函数关系式．

查看试题解析