2017年湖南省怀化市中考数学试卷
试卷更新日期：2017-07-03 类型：中考真卷
一、选择题
-
1. ﹣2的倒数是（ ）A、2 B、﹣2 C、﹣ D、2. 下列运算正确的是（ ）A、3m﹣2m=1 B、（m3）2=m6 C、（﹣2m）3=﹣2m3 D、m2+m2=m43. 为了贯彻习近平总书记提出的“精准扶贫”战略构想，怀化市2016年共扶贫149700人，将149700用科学记数法表示为（ ）A、1.497×105 B、14.97×104 C、0.1497×106 D、1.497×1064. 下列说法中，正确的是（ ）A、要了解某大洋的海水污染质量情况，宜采用全面调查方式 B、如果有一组数据为5，3，6，4，2，那么它的中位数是6 C、为了解怀化市6月15日到19日的气温变化情况，应制作折线统计图 D、“打开电视，正在播放怀化新闻节目”是必然事件5. 如图，直线a∥b，∠1=50°，则∠2的度数是（ ）
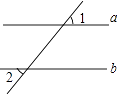A、130° B、50° C、40° D、150°6. 如图，在平面直角坐标系中，点A的坐标为（3，4），那么sinα的值是（ ）
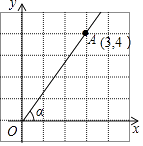A、 B、 C、 D、7. 若x1 ， x2是一元二次方程x2﹣2x﹣3=0的两个根，则x1•x2的值是（ ）A、2 B、﹣2 C、4 D、﹣38. 一次函数y=﹣2x+m的图象经过点P（﹣2，3），且与x轴、y轴分别交于点A、B，则△AOB的面积是（ ）A、 B、 C、4 D、89. 如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，AC=6cm，则AB的长是（ ）
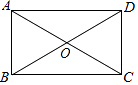A、3cm B、6cm C、10cm D、12cm10. 如图，A，B两点在反比例函数y= 的图象上，C，D两点在反比例函数y= 的图象上，AC⊥y轴于点E，BD⊥y轴于点F，AC=2，BD=1，EF=3，则k1﹣k2的值是（ ）
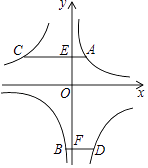A、6 B、4 C、3 D、2二、填空题
-
11. 因式分解：m2﹣m= ．12. 计算： = ．13. 如图，在▱ABCD中，对角线AC、BD相交于点O，点E是AB的中点，OE=5cm，则AD的长是 cm．
14. 如图，⊙O的半径为2，点A，B在⊙O上，∠AOB=90°，则阴影部分的面积为 ．
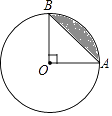15. 如图，AC=DC，BC=EC，请你添加一个适当的条件： ， 使得△ABC≌△DEC．
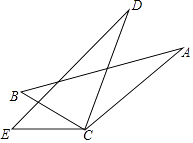16. 如图，在菱形ABCD中，∠ABC=120°，AB=10cm，点P是这个菱形内部或边上的一点．若以P，B，C为顶点的三角形是等腰三角形，则P，A（P，A两点不重合）两点间的最短距离为 cm．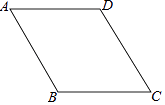
三、解答题
-
17. 计算：| ﹣1|+（2017﹣π）0﹣（ ）﹣1﹣3tan30°+ ．18. 解不等式组 ，并把它的解集在数轴上表示出来．19. 如图，四边形ABCD是正方形，△EBC是等边三角形．
(1)、求证：△ABE≌△DCE；(2)、求∠AED的度数．20. 为加强中小学生安全教育，某校组织了“防溺水”知识竞赛，对表现优异的班级进行奖励，学校购买了若干副乒乓球拍和羽毛球拍，购买2副乒乓球拍和1副羽毛球拍共需116元；购买3副乒乓球拍和2副羽毛球拍共需204元．(1)、求购买1副乒乓球拍和1副羽毛球拍各需多少元；(2)、若学校购买乒乓球拍和羽毛球拍共30幅，且支出不超过1480元，则最多能够购买多少副羽毛球拍？21. 先化简，再求值：（2a﹣1）2﹣2（a+1）（a﹣1）﹣a（a﹣2），其中a= +1．22. “端午节”是我国流传了上千年的传统节日，全国各地举行了丰富多彩的纪念活动，为了继承传统，减缓学生考前的心理压力，某班学生组织了一次拔河比赛，裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置，规则是：石头胜剪刀，剪刀胜布，布胜石头，手势相同则再决胜负．(1)、用列表或画树状图法，列出甲、乙两队手势可能出现的情况；(2)、裁判员的这种做法对甲、乙双方公平吗？请说明理由．23. 如图，已知BC是⊙O的直径，点D为BC延长线上的一点，点A为圆上一点，且AB=AD，AC=CD．
(1)、求证：△ACD∽△BAD；(2)、求证：AD是⊙O的切线．24.如图1，在平面直角坐标系中，已知抛物线y=ax2+bx﹣5与x轴交于A（﹣1，0），B（5，0）两点，与y轴交于点C．
(1)、求抛物线的函数表达式；(2)、若点D是y轴上的一点，且以B，C，D为顶点的三角形与△ABC相似，求点D的坐标；(3)、如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；
(4)、若点K为抛物线的顶点，点M（4，m）是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．