2017年天津市中考数学试卷

试卷更新日期：2017-07-03 类型：中考真卷

进入出卷网下载

一、选择题

1. 计算（﹣3）+5的结果等于（）

A、2 B、﹣2 C、8 D、﹣8

查看试题解析
2. cos60°的值等于（）

A、 $\sqrt{3}$ B、1 C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
3. 在一些美术字中，有的汉子是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 据《天津日报》报道，天津市社会保障制度更加成熟完善，截止2017年4月末，累计发放社会保障卡12630000张．将12630000用科学记数法表示为（）

A、0.1263×10⁸ B、1.263×10⁷ C、12.63×10⁶ D、126.3×10⁵

查看试题解析
5. 如图是一个由4个相同的正方体组成的立体图形，它的主视图是（）

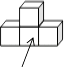A、 B、 C、 D、

查看试题解析
6. 估计 $\sqrt{38}$ 的值在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
7. 计算 $\frac{a}{a + 1} + \frac{1}{a + 1}$ 的结果为（）

A、1 B、a C、a+1 D、 $\frac{1}{a + 1}$

查看试题解析
8. 方程组 ${\begin{matrix} y = 2 x \\ 3 x + y = 15 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 4 \\ y = 3 \end{matrix}$ C、 ${\begin{matrix} x = 4 \\ y = 8 \end{matrix}$ D、 ${\begin{matrix} x = 3 \\ y = 6 \end{matrix}$

查看试题解析
9. 如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD．下列结论一定正确的是（）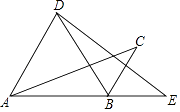

A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC

查看试题解析
10. 若点A（﹣1，y₁），B（1，y₂），C（3，y₃）在反比例函数 $y = - \frac{3}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₃＜y₁ C、y₃＜y₂＜y₁ D、y₂＜y₁＜y₃

查看试题解析
11.
如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（）

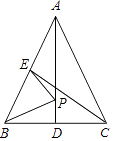A、BC B、CE C、AD D、AC

查看试题解析
12. 已知抛物线y=x²﹣4x+3与x轴相交于点A，B（点A在点B左侧），顶点为M．平移该抛物线，使点M平移后的对应点M'落在x轴上，点B平移后的对应点B'落在y轴上，则平移后的抛物线解析式为（）

A、y=x²+2x+1 B、y=x²+2x﹣1 C、y=x²﹣2x+1 D、y=x²﹣2x﹣1

查看试题解析

二、填空题

13. 计算x⁷÷x⁴的结果等于．

查看试题解析
14. 计算 $(4 + \sqrt{7}) (4 - \sqrt{7})$ 的结果等于．

查看试题解析
15. 不透明袋子中装有6个球，其中有5个红球、1个绿球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是红球的概率是．

查看试题解析
16. 若正比例函数y=kx（k是常数，k≠0）的图象经过第二、四象限，则k的值可以是（写出一个即可）．

查看试题解析
17. 如图，正方形ABCD和正方形EFCG的边长分别为3和1，点F，G分别在边BC，CD上，P为AE的中点，连接PG，则PG的长为．

查看试题解析
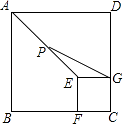18.
如图，在每个小正方形的边长为1的网格中，点A，B，C均在格点上．

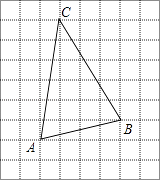(1)、AB的长等于；

(2)、在△ABC的内部有一点P，满足S_△_PAB：S_△_PBC：S_△_PCA=1：2：3，请在如图所示的网格中，用无刻度的直尺，画出点P，并简要说明点P的位置是如何找到的（不要求证明） $\underline{}$ ．

查看试题解析

三、解答题

19. 解不等式组 ${\begin{matrix} x + 1 \geq 2 ① \\ 5 x \leq 4 x + 3 ② \end{matrix}$
请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为．

查看试题解析
20.
某跳水队为了解运动员的年龄情况，作了一次年龄调查，根据跳水运动员的年龄（单位：岁），绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：

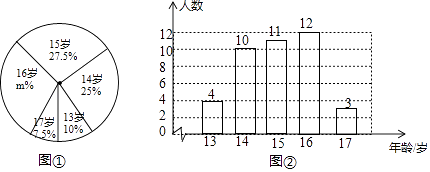(1)、本次接受调查的跳水运动员人数为，图①中m的值为；

(2)、求统计的这组跳水运动员年龄数据的平均数、众数和中位数．

查看试题解析
21. 已知AB是⊙O的直径，AT是⊙O的切线，∠ABT=50°，BT交⊙O于点C，E是AB上一点，延长CE交⊙O于点D．

(1)、如图①，求∠T和∠CDB的大小；

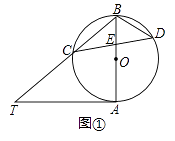(2)、如图②，当BE=BC时，求∠CDO的大小．

查看试题解析
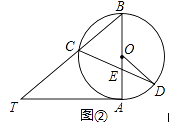22.
如图，一艘海轮位于灯塔P的北偏东64°方向，距离灯塔120海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，求BP和BA的长（结果取整数）．
参考数据：sin64°≈0.90，cos64°≈0.44，tan64°≈2.05， $\sqrt{2}$ 取1.414．

查看试题解析
23. 用A4纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元．在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元．
设在同一家复印店一次复印文件的页数为x（x为非负整数）．

(1)、根据题意，填写下表：
一次复印页数（页）
5
10
20
30
…
甲复印店收费（元）
0.5
2
…
乙复印店收费（元）
0.6
2.4
…

(2)、设在甲复印店复印收费y₁元，在乙复印店复印收费y₂元，分别写出y₁ ， y₂关于x的函数关系式；

(3)、当x＞70时，顾客在哪家复印店复印花费少？请说明理由．

查看试题解析
24. 将一个直角三角形纸片ABO放置在平面直角坐标系中，点 $A (\sqrt{3} ， 0)$ ，点B（0，1），点O（0，0）．P是边AB上的一点（点P不与点A，B重合），沿着OP折叠该纸片，得点A的对应点A'．

(1)、
如图①，当点A'在第一象限，且满足A'B⊥OB时，求点A'的坐标；

(2)、
如图②，当P为AB中点时，求A'B的长；

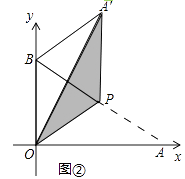(3)、当∠BPA'=30^°时，求点P的坐标（直接写出结果即可）．

查看试题解析
25. 已知抛物线y=x²+bx﹣3（b是常数）经过点A（﹣1，0）．

(1)、求该抛物线的解析式和顶点坐标；

(2)、P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．
①当点P'落在该抛物线上时，求m的值；
②当点P'落在第二象限内，P'A²取得最小值时，求m的值．

查看试题解析

一次复印页数（页）	5	10	20	30	…
甲复印店收费（元）	0.5		2		…
乙复印店收费（元）	0.6		2.4		…