初中数学人教版八年级上学期 第十三章测试卷
试卷更新日期：2019-10-15 类型：单元试卷
一、单选题
-
1. 下列图形中是轴对称图形的是（ ）A、
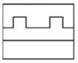B、
C、
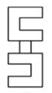D、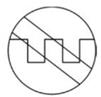
2. 如图，已知AB=AC，AB=5，BC=3，以AB两点为圆心，大于 AB的长为半径画圆弧，两弧相交于点M、N，连接MN与AC相交于点D，则△BDC的周长为（ ）
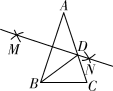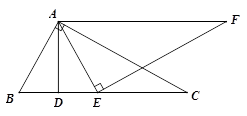
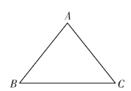
A、8 B、10 C、11 D、133. 如果P点的坐标为（a，b），它关于y轴的对称点为P1 ， P1关于x轴的对称点为P2 ， 已知P2的坐标为（﹣2，3），则点P的坐标为（ ）A、（﹣2，﹣3） B、（2，﹣3） C、（﹣2，3） D、（2，3）4. 如图在△ABC中，AB＝AC，AD是角平分线，BE＝CF，则下列说法正确的个数是（ ）( 1 )AD平分∠EDF；(2)△EBD≌△FCD；(3)BD＝CD；(4)AD⊥BC.
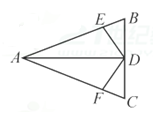A、1个 B、2个 C、3个 D、4个5. 如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，ED⊥AB于D.如果∠A＝30°，AE＝6cm，那么CE等于（ ）
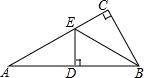A、 cm B、2cm C、3cm D、4cm6. 如图，在 中， ， ，点 在边 上，且 ，点 为 的中点，点 为边 上的动点，当点 在 上移动时，使四边形 周长最小的点 的坐标为（ ）
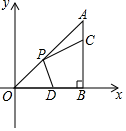A、 B、 C、 D、二、填空题
-
7. 点P（﹣2，9）与点Q关于x轴对称，则点Q的坐标是 ．8. 已知△ABC中，AB=AC=5，BC=6，D为平面内一点，若以A、B、C、D为顶点的四边形满足对角线互相垂直，且有一组对边相等，这个四边形的面积是 ．
9. 如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝60°，AB＝4，点D是BC上一动点，以BD为边在BC的右侧作等边△BDE，F是DE的中点，连结AF，CF，则AF+CF的最小值是 ．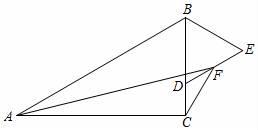
10. 如图，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是 ．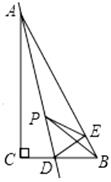
三、作图题
-
11. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（2，﹣1），B（1，﹣2），C（3，﹣3）
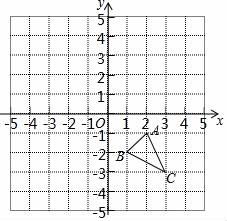
①将△ABC向上平移4个单位长度得到△A1B1C1 ， 请画出△A1B1C1；
②请画出与△ABC关于y轴对称的△A2B2C2；
③请写出A1、A2的坐标.
12. 如图，在边长为1个单位长度的小正方形组成的12×12的网格中，给出了以格点（网格线的交点）为端点的线段AB.
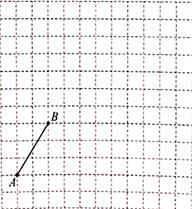(1)、将线段AB向右平移5个单位，再向上平移3个单位得到线段CD，请画出线段CD.
(2)、以线段CD为一边，作一个菱形CDEF，且点E，F也为格点.（作出一个菱形即可）四、综合题
-
13. 如图，在四边形ABCD中，AD=BC，∠A=∠B，E为AB的中点，连结CE，DE.
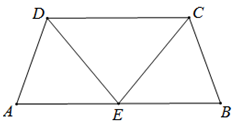(1)、求证：△ADE≌△BCE.(2)、若∠A＝70°，∠BCE＝60°，求∠CDE的度数．14. 如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE。
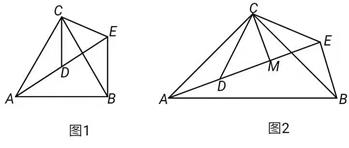(1)、求证：△ACD≌△BCE；(2)、求∠AEB的度数；(3)、如图2，△ACB和△DCE均为等腰直角三角形，且∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由。
