初中数学人教版八年级上学期 第十三章 13.3.4 课题学习 最短路径问题
试卷更新日期：2019-10-15 类型：同步测试
一、单选题
-
1. 如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=3，DC=1，点P是AB上的动点，则PC+PD的最小值为（ ）
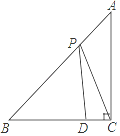A、4 B、5 C、6 D、72. 如图，点P是∠AOB内任意一点，∠AOB＝30°，OP＝8，点M和点N分别是射线OA和射线OB上的动点，则△PMN周长的最小值为（ ）
A、5 B、6 C、8 D、10二、填空题
-
3. 已知平面直角坐标系中A．B两点坐标如图，若PQ是一条在x轴上活动的线段，且PQ=1，求当BP+PQ+QA最小时，点Q的坐标.
4. 如图，等腰三角形ABC底边BC的长为4 cm，面积是12 cm2 ， 腰AB的垂直平分线EF交AG于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为cm.
5. 如图所示：点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1 ， P2 ， 连接P1P2交OA于M，交OB于N，△PMN的周长为15cm，P1P2＝ ．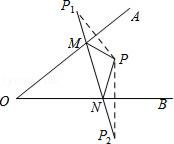
三、作图题
-
6. 图①、图②均是 的正方形网格，每个小正方形的顶点称为格点。点 、 、 、 均落在格点上.在图①、图②给定的网格中按要求作图.
(1)、在图①中的格线 上确定一点 ，使 与 的长度之和最小；(2)、在图②中的格线 上确定一点 ，使 .要求：只用无刻度的直尺，保留作图痕迹，不要求写出做法.
7. 如图，在平面直角坐标系中，点A（4，4），B（2，-4）．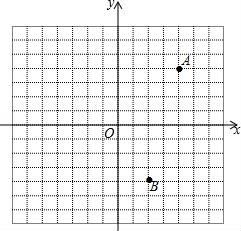
(1)、若点A关于x轴、y轴的对称点分别是点C、D，请分别描出并写出点C、D的坐标；(2)、在y轴上求作一点P，使PA+PB最小（不写作法，保留作图痕迹）四、综合题
-
8. 如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．
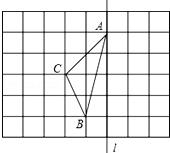(1)、在图中画出与△ABC关于直线l成轴对称的△AB′C′；(2)、求△ABC的面积为；(3)、在直线l上找一点P，使PB+PC的长最短，则这个最短长度为 ．9. A，B两所学校在一条东西走向公路的同旁，以公路所在直线为x轴建立如图所示的平面直角坐标系，且点A的坐标是(2，2)，点B的坐标是(7， 3)，根据下列要求作图（保留作图痕迹，不用写作法）.
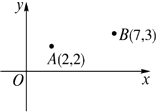(1)、一辆汽车由西向东行驶，在行驶过程中是否存在一点C，使C点到A，B两校的距离相等？如果有，请用尺规作图找出该点；(2)、若在公路边建一游乐场P，使游乐场到两校距离之和最小，通过作图在图中找出建游乐场P的位置，P点的坐标为.10. 如图A村和B村在一条大河CD的同侧，它们到河岸的距离AC、BD分别为1千米和4千米，又知道CD的长为4千米.
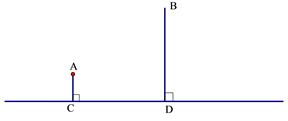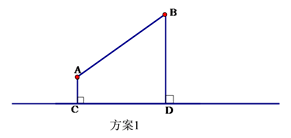
(1)、现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.方案1：水厂建在C点，修自来水管道到A村，再到B 村（即AC+AB）.（如图）
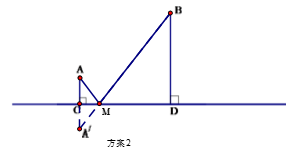
方案2：作A点关于直线CD的对称点 ，连接 交CD于M点，水厂建在M点处，分别向两村修管道AM和BM.（即AM+BM）（如图）
从节约建设资金方面考虑，将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算，判断哪种方案更合适.
(2)、有一艘快艇Q从这条河中驶过，当快艇Q与CD中点G相距多远时，△ABQ为等腰三角形？直接写出答案，不要说明理由.