初中数学人教版八年级上学期 第十三章 13.3.2 等边三角形
试卷更新日期:2019-10-15 类型:同步测试
一、基础巩固
-
1. 如右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,DE的长为( )
 A、7.4m B、3.7m C、1.85m D、2.85m2. 若等腰三角形的底角为15°,则一腰上的高是腰长的( )A、 B、 C、1倍 D、2倍3. 如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )
A、7.4m B、3.7m C、1.85m D、2.85m2. 若等腰三角形的底角为15°,则一腰上的高是腰长的( )A、 B、 C、1倍 D、2倍3. 如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( ) A、20° B、10° C、25° D、30°4. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=4,观察图中尺规作图的痕迹,则AD的长是( )
A、20° B、10° C、25° D、30°4. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=4,观察图中尺规作图的痕迹,则AD的长是( )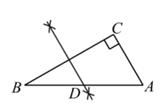 A、4 B、4 C、2 D、2
A、4 B、4 C、2 D、2二、强化提升
-
5. 在Rt△ABC中,∠C=90°,∠A=15°,AB的垂直平分线与AC交于点M,则BC与MB的比为( )A、1:3 B、1:2 C、2:3 D、3:46. 如图, 中, , ,小明要将该三角形分割成两个直角三角形和两个等腰三角形,他想出了如下方案:在 上取点 ,过点 画 交 于点 ,连结 ,在 上取合适的点 ,连结 可得到4个符合条件的三角形,则满足条件的 长是.
 7. 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,求AE的值.
7. 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,求AE的值.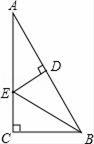 8. △ABC是等边三角形,P为平面内的一个动点,BP=BA,0º<∠PBC<180 º,DB平分∠PBC,且DB=DA.
8. △ABC是等边三角形,P为平面内的一个动点,BP=BA,0º<∠PBC<180 º,DB平分∠PBC,且DB=DA.
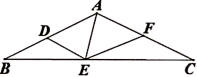
 (1)、当BP与BA重合时(如图1),求∠BPD的度数;(2)、当BP在∠ABC的内部时(如图2),求∠BPD的度数;(3)、当BP在∠ABC的外部时,请你直接写出∠BPD的度数.9. 如图, 和 都是等边三角形,BE和CD相交于点F.
(1)、当BP与BA重合时(如图1),求∠BPD的度数;(2)、当BP在∠ABC的内部时(如图2),求∠BPD的度数;(3)、当BP在∠ABC的外部时,请你直接写出∠BPD的度数.9. 如图, 和 都是等边三角形,BE和CD相交于点F. (1)、若 ,求BE的长;(2)、求证:AF平分 .10. 如图,在四边形ABCD中,AB=AD,AC是∠BAD的角平分线.
(1)、若 ,求BE的长;(2)、求证:AF平分 .10. 如图,在四边形ABCD中,AB=AD,AC是∠BAD的角平分线. (1)、求证:△ABC≌△ADC.(2)、若∠BCD=60°,AC=BC,求∠ADB的度数.
(1)、求证:△ABC≌△ADC.(2)、若∠BCD=60°,AC=BC,求∠ADB的度数.三、真题演练
-
11. 如图,等边 的边长为2,则点 的坐标为( )
 A、 B、 C、 D、12. 如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 =°
A、 B、 C、 D、12. 如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 =°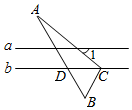 13. 如图,已知等边△ABC的边长为8,点P事AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
13. 如图,已知等边△ABC的边长为8,点P事AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.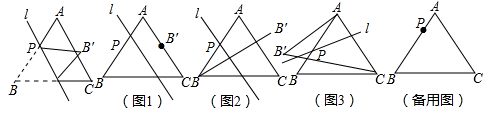 (1)、如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为;(2)、如图2,当PB=5时,若直线l∥AC,则BB’的长度为;(3)、如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)、当PB=6时,在直线l变化过程中,求△ACB’面积的最大值。
(1)、如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为;(2)、如图2,当PB=5时,若直线l∥AC,则BB’的长度为;(3)、如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)、当PB=6时,在直线l变化过程中,求△ACB’面积的最大值。