上海市浦东新区第三教育署2018-2019学年八年级上学期数学期末考试试卷(五四学制)
试卷更新日期:2019-10-15 类型:期末考试
一、选择题(本大题共6小题,共18.0分)
-
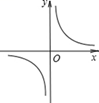
1. 下列各式中为最简二次根式的是( )A、 B、 C、 D、2. 化简 的结果是( )A、 B、 C、 D、3. 某市加大对绿化的投资,2015年绿化投资a万元,若以后每年绿化投资金额的年增长率均为x,则2017年绿化投资的金额为( )A、 B、 C、 D、4. 已知矩形的面积为10,则它的长与宽之间的函数关系用图象大致可表示为( )A、
 B、
B、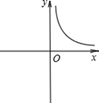 C、
C、 D、
D、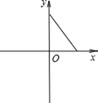 5. 已知△ABC内一点P,如果点P到AB、AC两边的距离相等,则点P( )A、在BC边的垂直平分线上 B、在BC边的高上 C、在BC边所对角的平分线上 D、在BC边的中线上6. 在函数y= (k>0)的图象上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),若x1>x2>0>x3 , 则下列各式中,正确的是( )A、 B、 C、 D、
5. 已知△ABC内一点P,如果点P到AB、AC两边的距离相等,则点P( )A、在BC边的垂直平分线上 B、在BC边的高上 C、在BC边所对角的平分线上 D、在BC边的中线上6. 在函数y= (k>0)的图象上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),若x1>x2>0>x3 , 则下列各式中,正确的是( )A、 B、 C、 D、二、填空题(本大题共12小题,共24.0分)
-
7. 已知f(x)= ,那么f(1)= .8. 函数 的定义域是 .9. 方程x2=8x的根是 .10. 化简: (b≥0)= .11. 经过点A且半径为1厘米的圆的圆心的轨迹是 .12. 命题“等腰三角形的两个底角相等.”的逆命题是 .13. 如果反比例函数y= 的图象在每个象限内y随x的增大而减小,那么k的取值范围是 .14. 已知函数y=(m-1)x+m2-1是正比例函数,则m= .15. 在实数范围内分解因式:3x2-6x+1= .16. 如果一个直角三角形的两条直角边的长分别为5、12,则斜边上的高的长度为 .17. 若关于x的一元二次方程a2x2+(2a-1)x+1=0有两个实数根,则a的取值范围是 .18. 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为(用含t的代数式表示).

三、计算题(本大题共1小题,共5.0分)
-
19. 解方程:(x-1)2-2(x-1)=15.
四、解答题(本大题共8小题,共53.0分)
-
20. 计算: +3 - .
21. 已知:∠O、点A及线段a(如图),求作:点P,使点P到∠O的两边的距离相等,且PA=a.(要求尺规作图,保留作图痕迹,不写作法). 22. 已知y=y1+y2 , y1与x2成正比例,y2与x-1成反比例,当x=-1时,y=3;当x=2时,y=-3,求y与x之间的函数关系式.23. 某药研究所开发了一种新药,在实际用药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示.
22. 已知y=y1+y2 , y1与x2成正比例,y2与x-1成反比例,当x=-1时,y=3;当x=2时,y=-3,求y与x之间的函数关系式.23. 某药研究所开发了一种新药,在实际用药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示. (1)、服药后小时,血液中含药量最高,达到每毫升毫克,接着逐渐减弱.(2)、服药后5小时,血液中含药量为每毫升毫克.(3)、当0≤x≤2时,y与x之间的函数关系式是 .(4)、如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个最有效时间x(小时)的范围是 .24. 把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE、AD,AD的延长线交BE于点F.
(1)、服药后小时,血液中含药量最高,达到每毫升毫克,接着逐渐减弱.(2)、服药后5小时,血液中含药量为每毫升毫克.(3)、当0≤x≤2时,y与x之间的函数关系式是 .(4)、如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个最有效时间x(小时)的范围是 .24. 把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE、AD,AD的延长线交BE于点F. (1)、求证:AD=BE;(2)、判断AF和BE的位置关系并说明理由.25. 已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
(1)、求证:AD=BE;(2)、判断AF和BE的位置关系并说明理由.25. 已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN. 26. 如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数 的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
26. 如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数 的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13. (1)、求反比例函数 和直线OE的函数解析式;(2)、求四边形OAFC的面积?27. 如图,在△ABC中,∠ACB=90°,∠A=30°,D是边AC上不与点A、C重合的任意一点,DE⊥AB,垂足为点E,M是BD的中点.
(1)、求反比例函数 和直线OE的函数解析式;(2)、求四边形OAFC的面积?27. 如图,在△ABC中,∠ACB=90°,∠A=30°,D是边AC上不与点A、C重合的任意一点,DE⊥AB,垂足为点E,M是BD的中点. (1)、求证:CM=EM;(2)、如果BC= ,设AD=x,CM=y,求y与x的函数解析式,并写出函数的定义域;(3)、当点D在线段AC上移动时,∠MCE的大小是否发生变化?如果不变,求出∠MCE的大小;如果发生变化,说明如何变化.
(1)、求证:CM=EM;(2)、如果BC= ,设AD=x,CM=y,求y与x的函数解析式,并写出函数的定义域;(3)、当点D在线段AC上移动时,∠MCE的大小是否发生变化?如果不变,求出∠MCE的大小;如果发生变化,说明如何变化.
-