上海市闵行区2018-2019学年九年级上学期数学期末考试试卷

试卷更新日期：2019-10-15 类型：期末考试

进入出卷网下载

一、选择题：（本大题共6题，每题4分，满分24分）

1. 在Rt△ABC中，∠C = 90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不成立的是（）

A、 $\tan B = \frac{b}{a}$ B、 $\cos B = \frac{a}{c}$ C、 $\sin A = \frac{a}{c}$ D、 $\cos A = \frac{a}{b}$

查看试题解析
2. 如果从甲船看乙船，乙船在甲船的南偏东30°方向，那么从乙船看甲船，甲船在乙船的（）

A、北偏东30° B、北偏西30° C、北偏东60° D、北偏西60°

查看试题解析
3. 将二次函数 $y = 2 {(x - 2)}^{2}$ 的图像向左平移1个单位，再向下平移3个单位后所得图像的函数解析式为（）

A、 $y = 2 {(x - 2)}^{2} - 4$ B、 $y = 2 {(x - 1)}^{2} + 3$ C、 $y = 2 {(x - 1)}^{2} - 3$ D、 $y = 2 x^{2} - 3$

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x + c$ 的图像如图所示，那么根据图像，下列判断中错误的是（）

A、a < 0 B、b > 0； C、c > 0； D、abc > 0．

查看试题解析
5. 已知：点C在线段AB上，且AC = 2BC，那么下列等式一定正确的是（）

A、 $\overset{⇀}{A C} + 2 \overset{⇀}{B C} = \frac{4}{3} \overset{⇀}{A B}$ B、 $\overset{⇀}{A C} - 2 \overset{⇀}{B C} = \overset{⇀}{0}$ C、 $| \overset{⇀}{A C} + \overset{⇀}{B C} | = | \overset{⇀}{B C} |$ D、 $| \overset{⇀}{A C} - \overset{⇀}{B C} | = | \overset{⇀}{B C} |$

查看试题解析
6. 已知在△ABC中，点D、E、F分别在边AB、AC和BC上，且DE∥BC，DF∥AC，那么下列比例式中，正确的是（）

A、 $\frac{A E}{E C} = \frac{C F}{F B}$ B、 $\frac{A E}{E C} = \frac{D E}{B C}$ C、 $\frac{D F}{A C} = \frac{D E}{B C}$ D、 $\frac{E C}{A C} = \frac{F C}{B C}$

查看试题解析

二、填空题：（本大题共12题，每题4分，满分48分）

7. 已知：x︰y = 2︰5，那么（x +y）︰y = ．

查看试题解析
8. 化简： $- \frac{3}{2} \overset{⇀}{a} + \overset{⇀}{b} + \frac{1}{2} (\overset{⇀}{a} - \frac{3}{2} \overset{⇀}{b}) =$ ．

查看试题解析
9. 抛物线 $y = x^{2} + 3 x + 2$ 与y轴的公共点的坐标是．

查看试题解析
10. 已知二次函数 $y = - \frac{1}{2} x^{2} - 3$ ，如果x > 0，那么函数值y随着自变量x的增大而．（填“增大”或“减小”）．

查看试题解析
11. 已知线段AB = 4厘米，点P是线段AB的黄金分割点（AP > BP），那么线段AP =厘米．（结果保留根号）

查看试题解析
12. 在△ABC中，点D、E分别在边AB、AC上，且DE // BC．如果 $\frac{A D}{A B} = \frac{3}{5}$ ，DE = 6，那么BC = ．

查看试题解析
13. 已知两个相似三角形的相似比为2︰3，那么这两个相似三角形的面积比为．

查看试题解析
14. 在Rt△ABC中，∠C = 90°， $A B = 2 \sqrt{10}$ ， $\tan A = \frac{1}{3}$ ，那么BC = ．

查看试题解析
15. 某超市自动扶梯的坡比为1︰2.4．一位顾客从地面沿扶梯上行了5.2米，那么这位顾客此时离地面的高度为米．

查看试题解析
16. 在△ABC和△DEF中， $\frac{A B}{D E} = \frac{B C}{E F}$ ．要使△ABC∽△DEF，还需要添加一个条件，那么这个条件可以是（只需填写一个正确的答案）．

查看试题解析
17. 如图，在Rt△ABC中，∠ACB = 90°， $A C = B C = 4 \sqrt{2}$ ，点D、E分别在边AB上，且AD = 2，∠DCE = 45°，那么DE = ．

查看试题解析
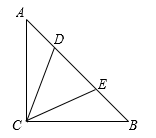18. 如图，在Rt△ABC中，∠ACB = 90°，BC = 3，AC = 4，点D为边AB上一点．将△BCD沿直线CD翻折，点B落在点E处，联结AE．如果AE // CD，那么BE = ．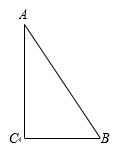

查看试题解析

三、解答题：（本大题共7题，满分78分）

19. 已知在平面直角坐标系xOy中，二次函数 $y = a x^{2} + b x + c$ 的图像经过点A（1，0）、B（0，-5）、C（2，3）．求这个二次函数的解析式，并求出其图像的顶点坐标和对称轴．

查看试题解析
20. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O．E为边AB上一点，且BE = 2AE．设 $\overset{⇀}{A B} = \overset{⇀}{a}$ ， $\overset{⇀}{A D} = \overset{⇀}{b}$ ．

(1)、求向量 $\overset{⇀}{D E}$

(2)、如果点F是线段OC的中点，求向量 $\overset{⇀}{E F}$ ，并在图中画出向量 $\overset{⇀}{E F}$ 在向量 $\overset{⇀}{A B}$ 和 $\overset{⇀}{A D}$ 方向上的分向量．
注：本题结果用向量 $\overset{⇀}{a} 、 \overset{⇀}{b}$ 的式子表示．画图不要求写作法，但要指出所作图中表示结论的向量．

查看试题解析
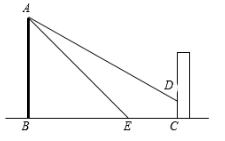
21. 如图，在Rt△ABC中，∠ACB = 90°，BC = 6，AC = 8．点D是AB边上一点，过点D作DE // BC，交边AC于E．过点C作CF // AB，交DE的延长线于点F．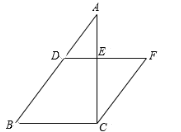

(1)、如果 $\frac{A D}{A B} = \frac{1}{3}$ ，求线段EF的长；

(2)、求∠CFE的正弦值．

查看试题解析
22. 如图，某公园内有一座古塔AB，在塔的北面有一栋建筑物，某日上午9时太阳光线与水平面的夹角为32°，此时塔在建筑物的墙上留下了高3米的影子CD．中午12时太阳光线与地面的夹角为45°，此时塔尖A在地面上的影子E与墙角C的距离为15米（B、E、C在一条直线上），求塔AB的高度．（结果精确到0.01米）
参考数据：sin32°≈0.5299，cos32°≈0.8480，tan32°≈0.6249， $\sqrt{2} \approx 1.4142$ ．

查看试题解析
23. 如图，在△ABC中，点D为边BC上一点，且AD＝AB，AE⊥BC，垂足为点E．过点D作DF∥AB，交边AC于点F，连接EF，EF²＝ $\frac{1}{2}$ BD•EC．

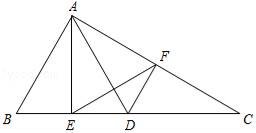(1)、求证：△EDF∽△EFC；

(2)、如果 $\frac{S_{Δ E D F}}{S_{Δ A D C}} = \frac{1}{4}$ ，求证：AB＝BD．

查看试题解析
24. 已知：在平面直角坐标系xOy中，抛物线 $y = a x^{2} + b x$ 经过点A（5，0）、B（-3，4），抛物线的对称轴与x轴相交于点D．

(1)、求抛物线的表达式；

(2)、联结OB、BD．求∠BDO的余切值；

(3)、如果点P在线段BO的延长线上，且∠PAO =∠BAO，求点P的坐标．

查看试题解析
25. 如图，在梯形ABCD中，AD // BC，AB = CD，AD = 5，BC = 15， $\cos ∠ A B C = \frac{5}{13}$ ．E为射线CD上任意一点，过点A作AF // BE，与射线CD相交于点F．联结BF，与直线AD相交于点G．设CE = x， $\frac{A G}{D G} = y$ ．

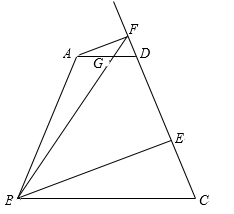(1)、求AB的长；

(2)、当点G在线段AD上时，求y关于x的函数解析式，并写出函数的定义域；

(3)、如果 $\frac{S_{四边形 A B E F}}{S_{四边形 A B C D}} = \frac{2}{3}$ ，求线段CE的长．

查看试题解析