上海虹口区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-10-15 类型:期末考试
一、选择题
-
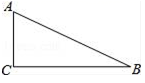
1. 抛物线 与 轴交点的坐标是( )A、(﹣1,0) B、(1,0) C、(0,﹣1) D、(0,1)2. 如果抛物线 开口向下,那么 的取值范围为( )A、 B、 C、 D、3. 如图,在 中, ,如果 , ,那么 的值为( )
 A、 B、 C、 D、4. 如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )
A、 B、 C、 D、4. 如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )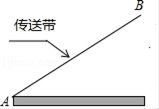 A、5 米 B、5 米 C、2 米 D、4 米5. 如果向量 与单位向量 的方向相反,且长度为3,那么用向量 表示向量 为( )A、 B、 C、 D、6. 如图,在 中, 平分 交 于点 ,点 在 上,如果 ,那么 与 的周长比为( )
A、5 米 B、5 米 C、2 米 D、4 米5. 如果向量 与单位向量 的方向相反,且长度为3,那么用向量 表示向量 为( )A、 B、 C、 D、6. 如图,在 中, 平分 交 于点 ,点 在 上,如果 ,那么 与 的周长比为( )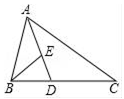 A、1:2 B、2:3 C、1:4 D、4:9
A、1:2 B、2:3 C、1:4 D、4:9二、填空题
-
7. 若 ,则 的值为.8. 计算: .9. 如果抛物线y=ax2+2经过点(1,0),那么a的值为 .10. 如果抛物线y=(m﹣1)x2有最低点,那么m的取值范围为 .11. 如果抛物线 的对称轴是直线 ,那么它的顶点坐标为 .12. 如果点 与点 都在抛物线 上,那么 (填“>”、“<”或“=”)13. 在 中, ,如果 , ,那么 .14. 如图, ,点 分别在 上,如果 ,那么 的长为 .
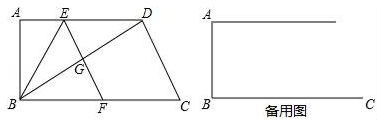
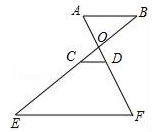 15. 如图,在 中,点 为 的重心,过点 作 分别交边 于点 ,过点 作 交 于点 ,如果 ,那么 的长为 .
15. 如图,在 中,点 为 的重心,过点 作 分别交边 于点 ,过点 作 交 于点 ,如果 ,那么 的长为 .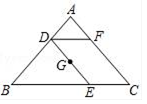 16. 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD交BC于点E , 如果AC=2,BC=4,那么cot∠CAE= .
16. 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD交BC于点E , 如果AC=2,BC=4,那么cot∠CAE= .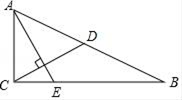 17. 定义:如果△ABC内有一点P , 满足∠PAC=∠PCB=∠PBA , 那么称点P为△ABC的布罗卡尔点,如图,在△ABC中,AB=AC=5,BC=8,点P为△ABC的布罗卡尔点,如果PA=2,那么PC= .
17. 定义:如果△ABC内有一点P , 满足∠PAC=∠PCB=∠PBA , 那么称点P为△ABC的布罗卡尔点,如图,在△ABC中,AB=AC=5,BC=8,点P为△ABC的布罗卡尔点,如果PA=2,那么PC= .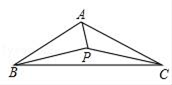 18. 如图,正方形 的边长为4,点 为对角线 的交点,点 为边 的中点, 绕着点 旋转至 ,如果点 在同一直线上,那么 的长为 .
18. 如图,正方形 的边长为4,点 为对角线 的交点,点 为边 的中点, 绕着点 旋转至 ,如果点 在同一直线上,那么 的长为 .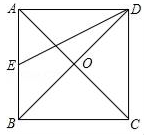
三、解答题
-
19. 计算: .20. 已知抛物线(1)、请用配方法求出顶点的坐标;(2)、如果该抛物线沿 轴向左平移 个单位后经过原点,求 的值.21. 如图,在 中, , , ,点 分别在边 上,且 , .
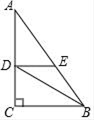 (1)、求 的长;(2)、如果 ,用 表示 .22. 如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与 上的线段 重合, 长为0.2米,当踏板连杆绕着点 旋转到 处时,测得 ,此时点 距离地面的高度 为0.45米,求 和 的长(参考数据: )
(1)、求 的长;(2)、如果 ,用 表示 .22. 如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与 上的线段 重合, 长为0.2米,当踏板连杆绕着点 旋转到 处时,测得 ,此时点 距离地面的高度 为0.45米,求 和 的长(参考数据: ) 23. 如图,在△ABC中,AB=AC , D是边BC的中点,DE⊥AC , 垂足为点 E .
23. 如图,在△ABC中,AB=AC , D是边BC的中点,DE⊥AC , 垂足为点 E .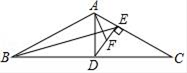 (1)、求证:DE•CD=AD•CE;(2)、设F为DE的中点,连接AF、BE , 求证:AF•BC=AD•BE .
(1)、求证:DE•CD=AD•CE;(2)、设F为DE的中点,连接AF、BE , 求证:AF•BC=AD•BE .