上海市静安区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-10-15 类型：期末考试

进入出卷网下载

一、选择题（本大题共6题,每题2分,满分12分）

1. 下列等式成立的是（）

A、 ${(- 1)}^{0} = - 1$ B、 ${(- 1)}^{0} = 1$ C、 $0^{- 1} = - 1$ D、 $0^{- 1} = 1$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{5} + a^{5} = a^{10}$ B、 $a^{5} \cdot a^{2} = a^{10}$ C、 $a^{5} \cdot a^{5} = a^{10}$ D、 ${(a^{5})}^{5} = a^{10}$

查看试题解析
3. 分式 $\frac{x + 1}{x - 1}$ 有意义的条件是（）

A、 $x = 1$ B、 $x \neq 1$ C、 $x = - 1$ D、 $x \neq - 1$

查看试题解析
4. 在下列代数式中，是整式的为（）

A、 $x + \frac{1}{x}$ B、 $3 x^{- 3}$ C、 $\frac{x^{2}}{x}$ D、 ${(- 3)}^{- 3}$

查看试题解析
5. 下列各式从左到右的变形，是因式分解且分解结果正确的为（）

A、 ${(a + 2)}^{2} - {(a - 1)}^{2} = 6 a + 3$ B、 $x^{2} + \frac{1}{4} x + \frac{1}{4} = {(x + \frac{1}{2})}^{2}$ C、 $x^{2} - x - 6 = (x - 3) (x + 2)$ D、 $x^{4} - 16 = (x^{2} + 4) (x^{2} - 4)$

查看试题解析
6. 下列说法中错误的是（）

A、轴对称图形只有一条对称轴 B、中心对称图形只有一个对称中心 C、成轴对称的两个图形只有一条对称轴 D、成中心对称的两个图形只有一个对称中心

查看试题解析

二、填空题（本大题共12题，每题3分，满分36分）

7. 分数 $\frac{3}{5}$ 的相反数是．

查看试题解析
8. 用科学记数法表示： $- 0.0000802 =$ ．

查看试题解析
9. 在小于等于9的正整数中任意取出一个数，取到素数的可能性大小是．

查看试题解析
10. 计算： ${(3 a b^{3})}^{2} =$ ．

查看试题解析
11. 分解因式： $a^{3} - a^{2} + a =$ ．

查看试题解析
12. 计算： $(4 a^{3} - a^{3}) \cdot a^{2} =$ ．

查看试题解析
13. 计算： $x \div (x^{2} + x) =$ ．

查看试题解析
14. 计算： $\frac{x}{x^{2} - y^{2}} - \frac{1}{x + y} =$ ．

查看试题解析
15. 计算： $(x^{- 1} + y^{- 1}) \div (x^{- 1} - y^{- 1}) =$

查看试题解析
16. 某商店9月份的销售额为 $a$ 万元，在10月份和11月份这两个月份中，此商店的销售额平均每月增长 $x %$ ，那么11月份此商店的销售额为万元（用含有 $a$ 、 $x$ 的代数式表示）．

查看试题解析
17. 下列图形由大小相等的等边三角形组成：图1为一个白三角形；图2在图1外部，画了3个黑三角形；图3在图2外部，画了6个白三角形；图4在图3外部，画了9个黑三角形；图5在图4外部，画了12个白三角形；……；以此类推，那么图 $n$ （ $n$ 为大于1的整数）在前一个图外部，画了个三角形（用含有 $n$ 的代数式表示）

查看试题解析
18. 如图，已知长方形 $A B C D$ 的边 $A B$ 长为 $a$ ，边 $A D$ 长为 $b$ ，长方形 $A B C D$ 绕点 $D$ 顺时针旋转 $90^{°}$ 后，点 $A$ 、 $B$ 、 $C$ 的对称点分别为 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ .用 $a$ 、 $b$ 的代数式表示三角形 $A B^{'} C$ 的面积为（结果化简）.

查看试题解析

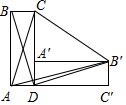
三、简答题（本大题共6题，第19-23题每题4分，第24题6分，满分26分）

19. 计算： ${(2 x - 3 y)}^{2} + (x - 2 y) (x + 2 y)$ .

查看试题解析
20. 分解因式： $x^{2} - 4 y^{2} + 4 - 4 x$ .

查看试题解析
21. 解方程： $\frac{1 - x}{x} + 1 = \frac{2}{x^{2} + x}$ .

查看试题解析
22. 先化简，再求值： $(\frac{1}{x^{2} - 2 x - 3} + \frac{1}{x^{2} - 6 x + 9}) \div \frac{x - 1}{x + 1}$ ，其中 $x = - 3$ .

查看试题解析
23. 已知三角形 $A B C$ 和直线 $l$ ，画出三角形 $A B C$ 关于直线 $l$ 成轴对称的三角形 $A^{'} B^{'} C^{'}$ .

查看试题解析
24. 已知圆环的面积为 $π$ ，其中大圆与小圆周长的和为 $4 π$ ，求圆环的宽度（大圆半径与小圆半径的差）.

查看试题解析

四、解答题（本大题共4题，第25-27每题6分，第28题8分，共26分）

25. 已知关于 $x$ 的多项式 $x^{2} + m x + n$ 与 $x^{2} - 2 x + 3$ 的积不含二次项和三次项，求常数 $m$ 、 $n$ 的值.

查看试题解析
26. 甲、乙两地间的铁路运行路程为1400千米，列车将原来运行的平均速度提高 $\frac{1}{3}$ 后，运行的时间减少 $\frac{5}{3}$ 小时，求列车原来运行的平均速度．

查看试题解析
27. 如图，将三角形 $A B C$ 沿射线 $B C$ 平移后能与三角形 $D E F$ 重合（点 $B$ 、 $C$ 分别与点 $E$ 、 $F$ 对应），如果 $B F$ 的长为12，点 $E$ 在边 $B C$ 上，且 $2 < E C < 4$ ，求边 $B C$ 长的取值范围.

查看试题解析
28. 在三角形 $A B C$ 中， $∠ A C B = 80^{°}$ （如图），将三角形 $A B C$ 绕着点 $C$ 逆时针旋转得到三角形 $D E C$ （点 $D$ 、 $E$ 分别与点 $A$ 、 $B$ 对应），如果 $∠ A C D$ 与 $∠ A C E$ 的度数之比为 $5 ： 3$ ，当旋转角大于 $0^{°}$ 且小于 $360^{°}$ 时，求旋转角的度数.

查看试题解析

上海市静安区2018-2019学年七年级上学期数学期末考试试卷

一、选择题（本大题共6题,每题2分,满分12分）

二、填空题（本大题共12题，每题3分，满分36分）

三、简答题 （本大题共6题，第19-23题每题4分，第24题6分，满分26分）

四、解答题（本大题共4题，第25-27每题6分，第28题8分，共26分）

三、简答题（本大题共6题，第19-23题每题4分，第24题6分，满分26分）