广东省肇庆市封开县2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期：2019-10-15 类型：期中考试
一、选择题：
-
1. 方程3x2﹣1=0的一次项系数是（ ）A、﹣1 B、0 C、3 D、12. 方程x（x﹣1）=0的根是（ ）A、x=0 B、x=1 C、x1=0，x2=1 D、x1=0，x2=﹣13. 抛物线y=2（x+1）2﹣3的对称轴是（ ）A、直线x=1 B、直线x=3 C、直线x=﹣1 D、直线x=﹣34. 下列所述图形中，是中心对称图形的是（ ）A、直角三角形 B、平行四边形 C、正五边形 D、正三角形5. 用配方法解一元二次方程x2﹣6x﹣10=0时，下列变形正确的为（ ）A、（x+3）2=1 B、（x﹣3）2=1 C、（x+3）2=19 D、（x﹣3）2=196. 如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使点A′恰好落在AB上，则旋转角度为（ ）
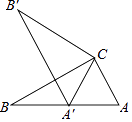A、30° B、45° C、60° D、90°7. 若关于x的方程x2+x﹣a+ =0有两个不相等的实数根，则实数a的取值范围是（ ）A、a＞2 B、a≥2 C、a≤2 D、a＜28. 三角形两边的长是3和4，第三边的长是方程x2﹣12x+35=0的根，则该三角形的周长为（ ）A、14 B、12 C、12或14 D、以上都不对9. 设二次函数y=（x﹣3）2﹣4图象的对称轴为直线l，若点M在直线l上，则点M的坐标可能是（ ）A、（1，0） B、（3，0） C、（﹣3，0） D、（0，﹣4）10. 二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（ ）
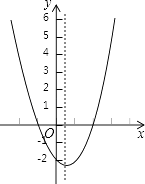A、函数有最小值 B、对称轴是直线x= C、当x＜ ，y随x的增大而减小 D、当﹣1＜x＜2时，y＞0二、填空题
-
11. 把方程2x2﹣1=5x化为一般形式是 ．12. 点P（﹣1，2）关于原点对称的点P′的坐标是 ．13. 若x=﹣1是一元二次方程x2+2x+a=0的一个根，那么a= ．14. 请写出一个开口向上，且其图象经过原点的抛物线的解析式 ．15. 已知点A（ ，y1），B（﹣2，y2）都在二次函数y=（x﹣2）2﹣1的图象上，则y1与y2的大小关系是 ．16. 如图，△ABC绕点A顺时针旋转45°得到△AB′C′，若∠BAC=90°，AB=AC= ，则图中阴影部分的面积等于 ．
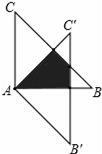
三、解答题（一）
-
17. 解方程：x2﹣3x+2=018. 已知二次函数y=﹣x2﹣2x，指出函数图象的对称轴和顶点坐标．19. 已知x=1是关于x的一元二次方程x2+3x﹣m=0的一个根，求m的值和方程的另一个根．
四、解答题（二）
-
20. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为（﹣1，1），B（﹣3，1），C（﹣1，4）．
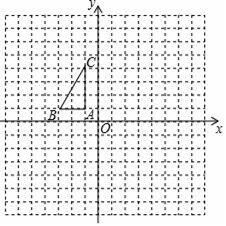(1)、将△ABC绕点A顺时针旋转90°后得到△AB′C′，请在图中画出△AB′C′．(2)、写出点B′、C′的坐标．21. 如图，已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B（点A在点B的左侧）．
(1)、求A、B的坐标；(2)、利用函数图象，写出y＜0时，x的取值范围．22. 向阳村2013年的人均收入为10000元，2015年人均收入为12100元，若2013年到2015年人均收入的年平均增长率相同．(1)、求人均收入的年平均增长率；(2)、2014年的人均收入是多少元？五、解答题（三）
-
23.
如图，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米2 ， 则修建的路宽应为多少米？
24. 一块三角形材料如图所示，∠A=30°，∠C=90°，AB=12，用这块材料剪出一个矩形CDEF，其中D、E、F分别在BC、AB、AC上．
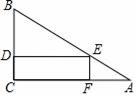(1)、若设AE=x，则AF=；（用含x的代数式表示）(2)、要使剪出的矩形CDEF的面积最大，点E应选在何处？25.如图，已知抛物线y=x2+bx+c与x轴交于点A、B，AB=2，与y轴交于点C，对称轴为直线x=2，对称轴交x轴于点M．
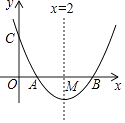(1)、求抛物线的函数解析式；(2)、设P为对称轴上一动点，求△APC周长的最小值；(3)、设D为抛物线上一点，E为对称轴上一点，若以点A、B、D、E为顶点的四边形是菱形，则点D的坐标为 ．