山东省滨州2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-10-15 类型：期中考试
一、选择题
-
1. 下列说法中正确的是（ ）A、三角形的角平分线、中线、高均在三角形内部 B、三角形中至少有一个内角不小于60° C、直角三角形仅有一条高 D、三角形的外角大于任何一个内角2. 如图，盖房子时，在窗框未安装之前，木工师傅常常先在窗框上斜钉一根木条，使其不变形，这种做法的根据是（ ）
A、两点之间，线段最短 B、三角形的稳定性 C、长方形的四个角都是直角 D、四边形的稳定性3. 在下列四个图案中，是轴对称图形的是（ ）
A、
B、
C、
D、
4. 已知一个三角形的两边长分别为3和4，则第三边的长不可能的是（ ）A、1 B、2 C、3 D、45. 如图，一副分别含有30°和45°角的两个直角三角板，拼成如图所示，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（ ）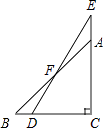
A、10° B、15° C、25° D、30°6. 如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，若∠A=26°，则∠CDE度数为（ ）
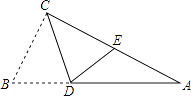A、71° B、64° C、80° D、45°7. 下列运算正确的是（ ）A、 B、 C、 D、8. 如右图，在△ABC中，线段BC的垂直平分线交线段AB于点D ， 若AC=CD ， ∠A=50°，则∠ACB的度数为（ ）
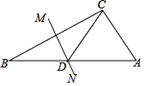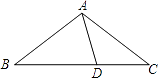
A、90° B、95° C、100° D、105°9. 在△ABC和△DEF中，已知∠C =∠D, ∠B =∠E,要判断这两个三角形全等，还需添加条件（ ）A、AB=ED. B、AB=FD. C、AC=FD. D、∠A =∠F.10.如图，在△ABC中，AB=AC，D为BC上一点，且DA=DC，BD=BA，则∠B的大小为（ ）
A、40° B、36° C、30° D、25°11. 如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当DPMN周长取最小值时，则∠MPN的度数为（ ）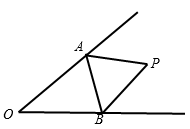
A、140° B、100° C、50° D、40°12. 如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E ， 使CE=2，连接DE ， 动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为（ ）秒时．△ABP和△DCE全等．
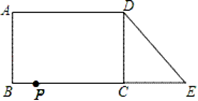A、1 B、1或3 C、1或7 D、3或7二、填空题
-
13. 已知点P(－2，1)，那么点P关于x轴对称的点P′的坐标是.14. 一个多边形的内角和等于1260°，它是边形．15. 如图所示，在△ABC中，∠B=90°，AB=3，BC=4，线段AC的垂直平分线DE交AC于D ， 交BC于E ， 连接AE ， 则△ABE的周长为 ．
16. （3xy2）2+（﹣4xy3）（﹣xy）=.17. 如图，在△ABC中，AD为∠BAC的平分线 ， DE⊥AB于点E ， DF⊥AC于点F ， △ABC的面积是28cm²，AB=16cm，AC=12cm， DE=.
18. 如图，在四边形ABCD中，AB=AD ， CB=CD ， 对角线AC ， BD相交于点O ， 下列结论中：
①∠ABC=∠ADC；②AC与BD相互平分；③AC，BD分别平分四边形ABCD的两组对角；④四边形ABCD的面积S= AC•BD ． 正确的是（填写所有正确结论的序号）
三、完成下列各题
-
19. 如图，有公路l1同侧、l2异侧的两个城镇A ， B ， 电信部门要在S区修建一座信号发射塔，按照设计要求，发射塔到两个城镇A ， B的距离必须相等，到两条公路l1 ， l2的距离也必须相等，发射塔C应修建在什么位置？请用尺规作图找出所有符合条件的点，注明点C的位置．(保留作图痕迹，不写作法)
20. △ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上．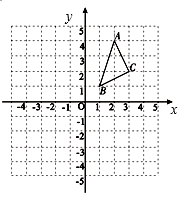
(1)、作出△ABC关于x轴对称的△A1B1C1 ， 并写出点C1的坐标；(2)、作出△ABC关于y对称的△A2B2C2 ， 并写出点C2的坐标．(3)、求△ABC的面积.21. 如图，四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E ， ∠ABC、∠BCD的角平分线交于点F ．
(1)、若∠F=70°，则∠ABC+∠BCD= °；∠E= °；(2)、探索∠E与∠F有怎样的数量关系，并说明理由；(3)、给四边形ABCD添加一个条件，使得∠E=∠F ， 所添加的条件为 ．22. 如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF.
(1)、求证：AD平分∠BAC；(2)、猜想写出AB＋AC与AE之间的数量关系并给予证明．23. 如图，△ABC中，AB=AC=4，∠B=∠C=40°．点D在线段BC上运动（点D不与B、C重合），连接AD ， 作∠ADE=40°，DE交线段AC于E ．
(1)、当∠BAD=20°时，∠EDC=°；(2)、当DC等于多少时，△ABD≌△DCE？试说明理由；(3)、△ADE能成为等腰三角形吗？若能，请直接写出此时∠BAD的度数；若不能，请说明理由．24. 如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E.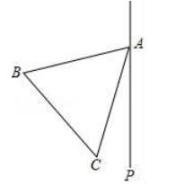
(1)、依题意补全图形；
(2)、若∠PAC＝20°，求∠AEB的度数；
(3)、连结CE，写出AE， BE， CE之间的数量关系，并证明你的结论．