初中数学人教版八年级上学期 第十三章 13.3.1 等腰三角形

试卷更新日期：2019-10-15 类型：同步测试

进入 出卷网 下载

一、基础巩固

  • 1. ΔABC 中， ∠A=∠B ，则 ΔABC 一定是（   ）
    A、锐角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

    查看试题解析

  • 2. 如图，一个长为2、宽为1的长方形以下面的“姿态”从直线 l 的左侧水平平移至右侧（下图中的虚线是水平线），其中，平移的距离是（   ）

    A、1 B、2 C、3 D、22

    查看试题解析

  • 3. 一个等腰三角形的周长为14,其一边长为4那么它的底边长为（   ）
    A、5 B、4 C、6 D、4或6

    查看试题解析

  • 4. 等腰三角形一个角为50°，它的另外两个角分别为 ．

    查看试题解析

二、强化提升

  • 5. 如图，在△ABC中，点D是BC边上一点，AD＝AC，过点D作DE⊥BC交AB于E，若△ADE是等腰三角形，则下列判断中正确的是（    ）

    A、∠B＝∠CAD B、∠BED＝∠CAD C、∠ADB＝∠AED D、∠BED＝∠ADC

    查看试题解析

  • 6. 在平面直角坐标系xOy中，已知点P（2，2），点Q在y轴上，△PQO是等腰三角形，则满足条件的点Q共有（   ）
    A、5个 B、4个 C、3个 D、2个

    查看试题解析

  • 7. 如图所示，AB＝BC＝CD＝DE＝EF＝FG，∠1＝125°，则∠A＝度.

    查看试题解析

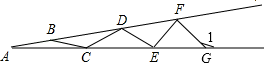  • 8. 如图，在△ABC中，AB=AC=3，∠B=50°，点D在BC边上（不与点B，C重合），连接AD，作∠ADE=50°，DE交边AC于点E.

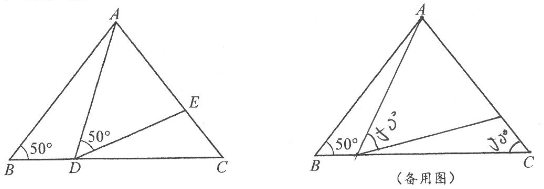    (1)、当∠BAD=20°时，求∠CDE的度数；
    (2)、当CD等于多少时，△ABD≌△DCE？为什么？
    (3)、在点D运动的过程中，△ADE可能是等腰三角形吗？若可能，直接写出∠DAE的度数；若不可能，说明理由.

    查看试题解析

  • 9. 如图，△ABC中，∠BAC＝90°，AD⊥BC，垂足为D．

    (1)、求作∠ABC的平分线，分别交AD，AC于P，Q两点；（要求：尺规作图，保留作图痕迹，不写作法）
    (2)、证明AP＝AQ．

    查看试题解析

  • 10. 已知：如图，AB＝AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，垂足为E.

    求证：AD＝AE.

    查看试题解析

三、真题演练

  • 11. 如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（   ）

    A、40° B、45° C、50° D、60°

    查看试题解析

  • 12. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（   ）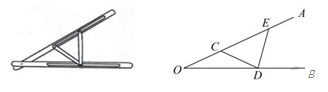

    A、60° B、65° C、75° D、80°

    查看试题解析

  • 13. 如图，AC，BD在AB的同侧，AC=2，BD=8，AB=8，点M为AB的中点，若∠CMD=120°，则CD的最大值是.

    查看试题解析

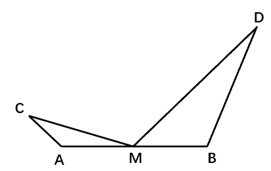  • 14. 如图，已知等腰△ABC顶角∠A＝36°.

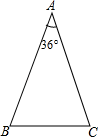    (1)、在AC上作一点D，使AD＝BD（要求：尺规作图，保留作图痕迹，不必写作法和证明，最后用黑色墨水笔加墨）；
    (2)、求证：△BCD是等腰三角形.

    查看试题解析

  • 15. 如图：

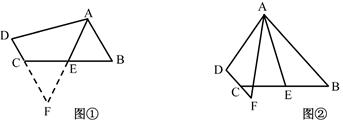    (1)、如图①，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系.

    解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC得到AB＝FC，从而把AB，AD，DC转化在一个三角形中即可判断.

    AB，AD，DC之间的等量关系；

    (2)、问题探究：如图②，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论.

    查看试题解析