2017年四川省绵阳市中考数学试卷
试卷更新日期:2017-06-30 类型:中考真卷
一、选择题
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期,﹣0.5的相反数是( )A、0.5 B、±0.5 C、﹣0.5 D、52. 下列图案中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 中国幅员辽阔,陆地面积约为960万平方公里,“960万”用科学记数法表示为( )A、0.96×107 B、9.6×106 C、96×105 D、9.6×1024. 如图所示的几何体的主视图正确的是( )
3. 中国幅员辽阔,陆地面积约为960万平方公里,“960万”用科学记数法表示为( )A、0.96×107 B、9.6×106 C、96×105 D、9.6×1024. 如图所示的几何体的主视图正确的是( )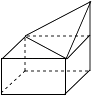 A、
A、 B、
B、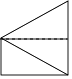 C、
C、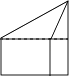 D、
D、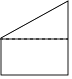 5. 使代数式 + 有意义的整数x有( )A、5个 B、4个 C、3个 D、2个6. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
5. 使代数式 + 有意义的整数x有( )A、5个 B、4个 C、3个 D、2个6. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( ) A、10m B、12m C、12.4m D、12.32m7. 关于x的方程2x2+mx+n=0的两个根是﹣2和1,则nm的值为( )A、﹣8 B、8 C、16 D、﹣168. “赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图,已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )
A、10m B、12m C、12.4m D、12.32m7. 关于x的方程2x2+mx+n=0的两个根是﹣2和1,则nm的值为( )A、﹣8 B、8 C、16 D、﹣168. “赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图,已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )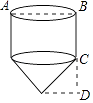 A、68πcm2 B、74πcm2 C、84πcm2 D、100πcm29. 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ,∠AEO=120°,则FC的长度为( )
A、68πcm2 B、74πcm2 C、84πcm2 D、100πcm29. 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ,∠AEO=120°,则FC的长度为( ) A、1 B、2 C、 D、10. 将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )A、b>8 B、b>﹣8 C、b≥8 D、b≥﹣811.
A、1 B、2 C、 D、10. 将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )A、b>8 B、b>﹣8 C、b≥8 D、b≥﹣811.如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则 的值为( )
 A、 B、 C、 D、12.
A、 B、 C、 D、12.如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 + + +…+ 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
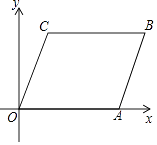
13. 分解因式:8a2﹣2= .14. 关于x的分式方程 = 的解是 .15. 如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是 .
 16. 同时抛掷两枚质地均匀的骰子,则事件“两枚骰子的点数和小于8且为偶数”的概率是 .17. 将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+ 的最小值为 .
16. 同时抛掷两枚质地均匀的骰子,则事件“两枚骰子的点数和小于8且为偶数”的概率是 .17. 将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+ 的最小值为 .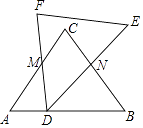 18. 如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ,则 的值是 .
18. 如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ,则 的值是 .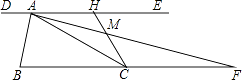
三、解答题
-
19. 计算题
(1)、计算: +cos245°﹣(﹣2)﹣1﹣|﹣ |(2)、先化简,再求值:( ﹣ )÷ ,其中x=2 ,y= .20. 红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):182
195
201
179
208
204
186
192
210
204
175
193
200
203
188
197
212
207
185
206
188
186
198
202
221
199
219
208
187
224
(1)、对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数
175≤x<185
185≤x<195
195≤x<205
205≤x<215
215≤x<225
频数
8
10
3
对应扇形图中区域
D
E
C
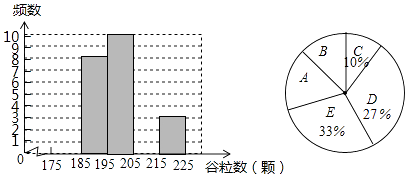
如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)、该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?21. 江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.(1)、每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?(2)、大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.22. 如图,设反比例函数的解析式为y= (k>0).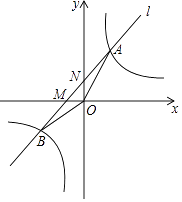 (1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.23. 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.23. 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.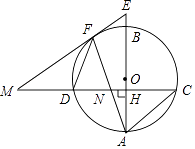 (1)、求证:CA=CN;(2)、连接DF,若cos∠DFA= ,AN=2 ,求圆O的直径的长度.24.
(1)、求证:CA=CN;(2)、连接DF,若cos∠DFA= ,AN=2 ,求圆O的直径的长度.24.如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y= x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
 (1)、求抛物线的解析式;(2)、证明:圆C与x轴相切;(3)、过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值.25.
(1)、求抛物线的解析式;(2)、证明:圆C与x轴相切;(3)、过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值.25.如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
 (1)、在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;(2)、求y关于t的函数解析式及相应t的取值范围;(3)、当y取最大值时,求sin∠NEF的值.
(1)、在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;(2)、求y关于t的函数解析式及相应t的取值范围;(3)、当y取最大值时,求sin∠NEF的值.