2017年江苏省徐州市中考数学试卷
试卷更新日期:2017-06-30 类型:中考真卷
一、选择题
-
1. ﹣5的倒数是( )A、﹣5 B、5 C、 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、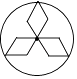 C、
C、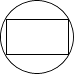 D、
D、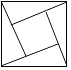 3. 肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )A、7.1×107 B、0.71×10﹣6 C、7.1×10﹣7 D、71×10﹣84. 下列运算正确的是( )A、a﹣(b+c)=a﹣b+c B、2a2•3a3=6a5 C、a3+a3=2a6 D、(x+1)2=x2+15. 在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动,为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
3. 肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )A、7.1×107 B、0.71×10﹣6 C、7.1×10﹣7 D、71×10﹣84. 下列运算正确的是( )A、a﹣(b+c)=a﹣b+c B、2a2•3a3=6a5 C、a3+a3=2a6 D、(x+1)2=x2+15. 在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动,为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:册数
0
1
2
3
4
人数
4
12
16
17
1
关于这组数据,下列说法正确的是( )
A、中位数是2 B、众数是17 C、平均数是2 D、方差是26. 如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )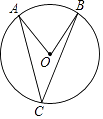 A、28° B、54° C、18° D、36°7. 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y= (m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b> 的解集为( )
A、28° B、54° C、18° D、36°7. 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y= (m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b> 的解集为( )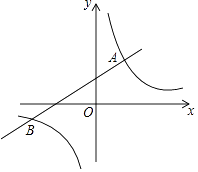 A、x<﹣6 B、﹣6<x<0或x>2 C、x>2 D、x<﹣6或0<x<28. 若函数y=x2﹣2x+b的图象与坐标轴有三个交点,则b的取值范围是( )A、b<1且b≠0 B、b>1 C、0<b<1 D、b<1
A、x<﹣6 B、﹣6<x<0或x>2 C、x>2 D、x<﹣6或0<x<28. 若函数y=x2﹣2x+b的图象与坐标轴有三个交点,则b的取值范围是( )A、b<1且b≠0 B、b>1 C、0<b<1 D、b<1二、填空题
-
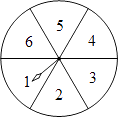
9. 4的算术平方根是 .10. 如图,转盘中6个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向的数小于5的概率为 .
 11. 使 有意义的x的取值范围是 .12. 反比例函数y= 的图象经过点M(﹣2,1),则k= .13. △ABC中,点D,E分别是AB,AC的中点,DE=7,则BC= .14. 已知a+b=10,a﹣b=8,则a2﹣b2= .15. 正六边形的每个内角等于°.16. 如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=°.
11. 使 有意义的x的取值范围是 .12. 反比例函数y= 的图象经过点M(﹣2,1),则k= .13. △ABC中,点D,E分别是AB,AC的中点,DE=7,则BC= .14. 已知a+b=10,a﹣b=8,则a2﹣b2= .15. 正六边形的每个内角等于°.16. 如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=°.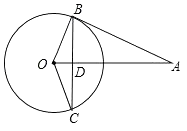 17. 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
17. 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .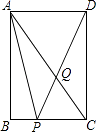 18. 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .
18. 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .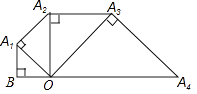
三、解答题
-
19. 计算:(1)、(﹣2)2﹣( )﹣1+20170(2)、(1+ )÷ .20.(1)、解方程: =(2)、解不等式组: .21.
某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽查部分学生做了一次问卷调查,要求学生选出自己最喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
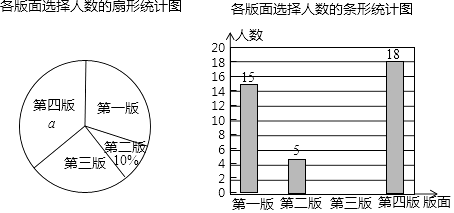
请根据图中信息,解答下列问题:
(1)、该调查的样本容量为 , a=%,“第一版”对应扇形的圆心角为°;(2)、请你补全条形统计图;(3)、若该校有1000名学生,请你估计全校学生中最喜欢“第三版”的人数.22. 一个不透明的口袋中装有4张卡片,卡片上分别标有数字1,﹣3,﹣5,7,这些卡片数字外都相同,小芳从口袋中随机抽取一张卡片,小明再从剩余的三张卡片中随机抽取一张,请你用画树状图或列表的方法,求两人抽到的数字符号相同的概率.23. 如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.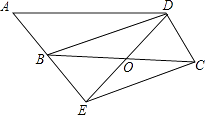 (1)、求证:四边形BECD是平行四边形;(2)、若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.24. 4月9日上午8时,2017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他的两个孩子一同参加了比赛,下面是两个孩子与记者的对话:
(1)、求证:四边形BECD是平行四边形;(2)、若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.24. 4月9日上午8时,2017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他的两个孩子一同参加了比赛,下面是两个孩子与记者的对话: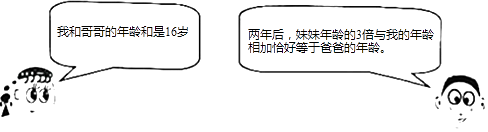
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
25. 如图,已知AC⊥BC,垂足为C,AC=4,BC=3 ,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.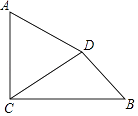 (1)、线段DC=;(2)、求线段DB的长度.26.
(1)、线段DC=;(2)、求线段DB的长度.26.如图①,菱形ABCD中,AB=5cm,动点P从点B出发,沿折线BC﹣CD﹣DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停止,它们运动的速度相同,设点P出发xs时,△BPQ的面积为ycm2 , 已知y与x之间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分,请根据图中的信息,解答下列问题:
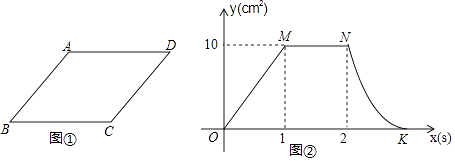 (1)、当1<x<2时,△BPQ的面积(填“变”或“不变”);(2)、分别求出线段OM,曲线NK所对应的函数表达式;(3)、当x为何值时,△BPQ的面积是5cm2?27.
(1)、当1<x<2时,△BPQ的面积(填“变”或“不变”);(2)、分别求出线段OM,曲线NK所对应的函数表达式;(3)、当x为何值时,△BPQ的面积是5cm2?27.如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.
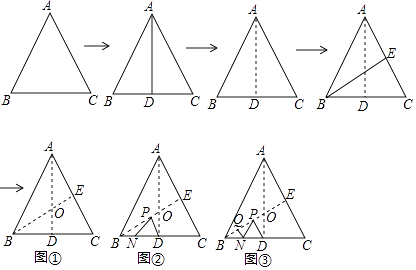 (1)、探求AO到OD的数量关系,并说明理由;(2)、如图②,若P,N分别为BE,BC上的动点.
(1)、探求AO到OD的数量关系,并说明理由;(2)、如图②,若P,N分别为BE,BC上的动点.(Ⅰ)当PN+PD的长度取得最小值时,求BP的长度;
(Ⅱ)如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= .
28.如图,已知二次函数y= x2﹣4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为 ,P为⊙C上一动点.
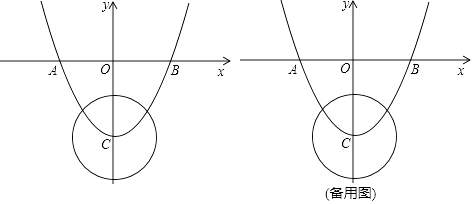 (1)、点B,C的坐标分别为B(),C();(2)、是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)、连接PB,若E为PB的中点,连接OE,则OE的最大值= .
(1)、点B,C的坐标分别为B(),C();(2)、是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)、连接PB,若E为PB的中点,连接OE,则OE的最大值= .