初中数学北师大版九年级上学期 第二章 2.6 应用一元二次方程
试卷更新日期：2019-10-12 类型：同步测试
一、单选题
-
1. 扬帆中学有一块长30m.宽20m的矩形空地，计划在这块空地上划出四分之—的区域种花.小禹同学设计方案如图所示.求花带的宽度。设花带的宽度为x m.则可列方程为（ ）
A、(30-x)(20-x)= ×20×30 B、(30-2x)(20-x)= ×20×30 C、30x+2×20x= ×20×30 D、(30-2x)(20-x)= ×20×302. 将一块长方形桌布铺在长为3m，宽为2m的长方形桌面上，各边下垂的长度相同，且桌布的面积是桌面面积的2倍，求桌布下垂的长度．设桌布下垂的长度为xm，则所列的方程是（ ）A、（2x+3）（2x+2)=2×3×2 B、2（x+3)（x+2)=3×2 C、(x+3）（x+2)=2×3×2 D、2(2x+3）(2x+2)=3×2 21/4x3. 某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是 ，则这种植物每个支干长出的小分支个数是（ ）A、 B、 C、 D、4. 如图，空地上（空地足够大）有一段长为20m的旧墙MN，小敏利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长100m，矩形菜园ABCD的面积为900m2 ． 若设AD＝xm，则可列方程（ ）
A、（50﹣ ）x＝900 B、（60﹣x）x＝900 C、（50﹣x）x＝900 D、（40﹣x）x＝900二、解答题
-
5. 某地计划对矩形广场进行扩建改造.如图，原广场长50m，宽40m，要求扩充后的矩形广场长与宽的比为3：2.扩充区域的扩建费用每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用每平方米100元.如果计划总费用642000元，扩充后广场的长和宽应分别是多少米？
6. 如图，有一块矩形硬纸板，长 ，宽 .在其四角各剪去一个同样的正方形，然后将四周突出部分折起，可制成一个无盖长方体盒子.当剪去正方形的边长取何值时，所得长方体盒子的侧面积为 ？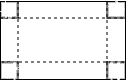
三、综合题
-
7. 已知y=ax2+bx+1，当x=1时，y=0;当x=2时，y=3．(1)、求a、b的值(2)、当x=-2时，求y的值8. 安顺市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量y（千元）与每千元降价x（元）（0<x<20）之间满足一次函数关系，其图象如图所示：
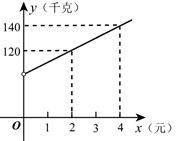(1)、求y与x之间的函数关系式；(2)、商贸公司要想获利2090元，则这种干果每千克应降价多少元？9. 一家水果店以每千克2元的价格购进某种水果若干千克，然后以每千克4元的价格出售，每天可售出100千克，通过调查发现，这种水果每千克的售价每降低1元，每天可多售出200千克．(1)、若将这种水果每千克的售价降低 元，则每天销售量是多少千克？（结果用含 的代数式表示）(2)、若想每天盈利300元，且保证每天至少售出260千克，那么水果店需将每千克的售价降低多少元？10. 某商场在去年底以每件80元的进价购进一批同型号的服装，一月份以每件150元的售价销售了320件，二、三月份该服装畅销，销量持续走高，在售价不变的情况下，三月底统计知三月份的销量达到了500件(1)、求二、三月份服装销售量的平均月增长率(2)、从四月份起商场因换季清仓采用降价促销的方式，经调查发现，在三月份销量的基础上，该服装售价每降价5元，月销售量增加10件，当每件降价多少元时，四月份可获利12000元?