2017年浙江省温州市乐清市中考数学模拟试卷
试卷更新日期:2017-06-29 类型:中考模拟
一、选择题
-
1. 计算(﹣1)×1的结果是( )A、﹣1 B、0 C、1 D、﹣22. 下列图形既是轴对称图形,又是中心对称图形的是( )A、等边三角形 B、平行四边形 C、梯形 D、矩形3. 若a>b,则下列各式中一定成立的是( )A、a+2<b+2 B、a﹣2<b﹣2 C、 >
 D、﹣2a>﹣2b
4. 我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )A、134石 B、169石 C、338石 D、1365石5. 小明对某校九年级所有同学校本课程选修情况进行了调查,把所得数据绘制成如图所示的扇形统计图.已知参加巧手园地的为30人,则参加趣味足球的人数是( )
D、﹣2a>﹣2b
4. 我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )A、134石 B、169石 C、338石 D、1365石5. 小明对某校九年级所有同学校本课程选修情况进行了调查,把所得数据绘制成如图所示的扇形统计图.已知参加巧手园地的为30人,则参加趣味足球的人数是( ) A、35 B、48 C、52 D、706.
A、35 B、48 C、52 D、706.如图,等边△AOB中,点B在x轴正半轴上,点A坐标为(1, ),将△AOB绕点O逆时针旋转30°,此时点A对应点A′的坐标是( )
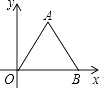 A、(0, ) B、(2,0) C、(0,2) D、( ,1)7. 关于x的分式方程
A、(0, ) B、(2,0) C、(0,2) D、( ,1)7. 关于x的分式方程 的解是负数,则m的取值范围是( ) A、m>﹣1 B、m>﹣1且m≠0 C、m≥﹣1 D、m≥﹣1且m≠08. 如图,已知点A、B分别是反比例函数y= (x>0),y=
的解是负数,则m的取值范围是( ) A、m>﹣1 B、m>﹣1且m≠0 C、m≥﹣1 D、m≥﹣1且m≠08. 如图,已知点A、B分别是反比例函数y= (x>0),y= (x<0)的图象上的点,且,∠AOB=90°,则
(x<0)的图象上的点,且,∠AOB=90°,则 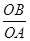 的值为( )
的值为( ) 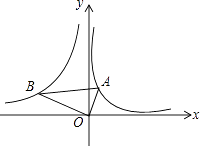 A、4 B、 C、2 D、9. 函数y=ax2+bx+3,当x=1与x=2016时,函数值相等,则当x=2017时,函数值等于( )A、3 B、﹣ C、 D、﹣310. 如图,在平面直角坐标系中,矩形ABCD的面积为定值,它的对称中心恰与原点重合,且AB∥y轴,CD交x轴于点M,过原点的直线EF分别交AD、BC边于点E、F,以EF为一边作矩形EFGH,并使EF的对边GH所在直线过点M,若点A的横坐标逐渐增大,图中矩形EFGH的面积的大小变化情况是( )
A、4 B、 C、2 D、9. 函数y=ax2+bx+3,当x=1与x=2016时,函数值相等,则当x=2017时,函数值等于( )A、3 B、﹣ C、 D、﹣310. 如图,在平面直角坐标系中,矩形ABCD的面积为定值,它的对称中心恰与原点重合,且AB∥y轴,CD交x轴于点M,过原点的直线EF分别交AD、BC边于点E、F,以EF为一边作矩形EFGH,并使EF的对边GH所在直线过点M,若点A的横坐标逐渐增大,图中矩形EFGH的面积的大小变化情况是( )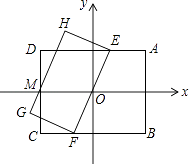 A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小
A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小二、填空题
-
11. 已知圆锥底面半径为1,母线为2,则它的侧面积为 .12. 不等式组
 的解集是 . 13. 太极是中国文化史上的一个重要概念.如图是太极图,是以大圆直径AB分别向左右作两个半圆而成,若AB=10cm,记
的解集是 . 13. 太极是中国文化史上的一个重要概念.如图是太极图,是以大圆直径AB分别向左右作两个半圆而成,若AB=10cm,记 ,
,  ,
,  的长分别为l1 , l2 , l3 , 则l1+l2+l3=cm.
的长分别为l1 , l2 , l3 , 则l1+l2+l3=cm.  14. 因式分解:a3﹣a= .15. 如图,Rt△ABC中,∠ACB=90°,点D,E分别是AB,BC上的点,且满足AC=DC=DE=BE=1,则tanA= .
14. 因式分解:a3﹣a= .15. 如图,Rt△ABC中,∠ACB=90°,点D,E分别是AB,BC上的点,且满足AC=DC=DE=BE=1,则tanA= . 16. 如图,点A和点F,点B和点E分别是反比例函数y= 图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 .
16. 如图,点A和点F,点B和点E分别是反比例函数y= 图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 .
三、解答题
-
17. 计算下列各题(1)、计算:2sin30°+ ﹣20170(2)、化简:(2a+1)2﹣a(4a+2)18. 关于x的一元二次方程2x2﹣4x+m=0,(1)、已知x=3是方程的解,求m;(2)、若方程有两个不相等的实数根,求m的取值范围.19. 一个不透明的口袋中装有红、白两种颜色的小球(除颜色外其余都相同),其中红球3个,白球1个.(1)、求任意摸出一球是白球的概率;(2)、甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用画树状图或列表的方法求两次摸出都是红球的概率.20. 如图,在▱ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
 (1)、求证:△ADE≌△CBF;(2)、若∠ADB是直角,请证明四边形BEDF是菱形.21. 如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E.
(1)、求证:△ADE≌△CBF;(2)、若∠ADB是直角,请证明四边形BEDF是菱形.21. 如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E.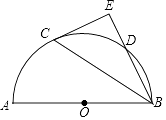 (1)、求证:CE是半圆的切线;(2)、若OB=5,BC=8,求CE的长.22.
(1)、求证:CE是半圆的切线;(2)、若OB=5,BC=8,求CE的长.22. (1)、当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?(2)、当标价总额是多少时,甲、乙超市实付款一样?(3)、小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?23.
(1)、当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?(2)、当标价总额是多少时,甲、乙超市实付款一样?(3)、小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?23.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
 (1)、求点A,B,C的坐标.(2)、当点M恰好是EF的中点,求BD的长.(3)、连接DE,记△DEM,△BDE的面积分别为S1 , S2 , 当BD=1时,则S2﹣S1= .24. 如图1,在边长为5的菱形ABCD中,cos∠BAD= ,点E是射线AB上的点,作EF⊥AB,交AC于点F.
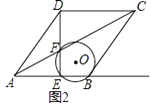
(1)、求点A,B,C的坐标.(2)、当点M恰好是EF的中点,求BD的长.(3)、连接DE,记△DEM,△BDE的面积分别为S1 , S2 , 当BD=1时,则S2﹣S1= .24. 如图1,在边长为5的菱形ABCD中,cos∠BAD= ,点E是射线AB上的点,作EF⊥AB,交AC于点F.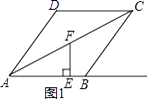 (1)、求菱形ABCD的面积;(2)、求证:AE=2EF;(3)、如图2,过点F,E,B作⊙O,连结DF,若⊙O与△CDF的边所在直线相切,求所有满足条件的AE的长度.
(1)、求菱形ABCD的面积;(2)、求证:AE=2EF;(3)、如图2,过点F,E,B作⊙O,连结DF,若⊙O与△CDF的边所在直线相切,求所有满足条件的AE的长度.