2017年浙江省杭州市大江东区中考数学一模试卷
试卷更新日期:2017-06-29 类型:中考模拟
一、选择题:
-
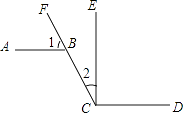
1. 下列各数中,能化为无限不循环小数的是( )A、 B、 C、 D、2. 下列二次根式中,最简二次根式的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、x3+x2=x5 B、x3﹣x2=x C、(x3)2=x5 D、x3÷x2=x4. 下列命题中,真命题是( )A、周长相等的锐角三角形都全等 B、周长相等的等腰直角三角形都全等 C、周长相等的钝角三角形都全等 D、周长相等的直角三角形都全等5. 如图,AB∥CD,EC⊥CD于C,CF交AB于B,已知∠2=29°,则∠1的度数是( )
 A、58° B、59° C、61° D、62°6. 在社会实践活动中,某中学对甲、乙,丙、丁四个超市三月份的苹果价格进行调查.它们的价格的平均值均为3.50元,方差分别为S甲2=0.3,
A、58° B、59° C、61° D、62°6. 在社会实践活动中,某中学对甲、乙,丙、丁四个超市三月份的苹果价格进行调查.它们的价格的平均值均为3.50元,方差分别为S甲2=0.3,S乙2=0.4,S丙2=0.1,S丁2=0.25.三月份苹果价格最稳定的超市是( )
A、甲 B、乙 C、丙 D、丁7. 小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了 ,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )A、 = × B、 = × C、 + = D、 ﹣ =8. 已知:点P到直线l的距离为3,以点P为圆心,r为半径画圆,如果圆上有且只有两点到直线L的距离均为2,则半径r的取值范围是( )A、r>1 B、r>2 C、2<r<2 D、1<r<59. 如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则sin∠BAC的值( )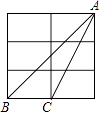 A、 B、 C、 D、10. 如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )
A、 B、 C、 D、10. 如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )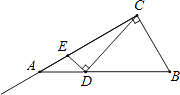 A、
A、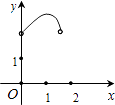 B、
B、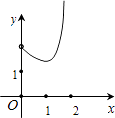 C、
C、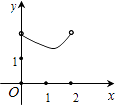 D、
D、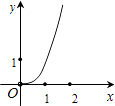
二、填空题:
-
11. 若分式 的值为0,则x的值等于 .12. 同时掷两个质地均匀的骰子,观察向上一面的点数,两个骰子的点数相同的概率为 .13. 规定用符号[m]表示一个实数m的整数部分,例如:[ ]=0,[3.14]=3.按此规定,则[ + ]的值为 .14. 已知三个数1, ,2,请再添上一个数,使它们构成一个比例式,满足这样条件的数是 .15. 如图,直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(﹣1,0)和B(3,0)两点.则不等式组k1x+b>k2x+b>0的解集为 .
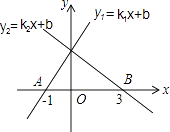 16. 如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④ 为常量.其中正确的有 .
16. 如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④ 为常量.其中正确的有 .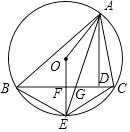
三、解答题:
-
17. 如果用c表示摄氏温度,f表示华氏温度,则c与f之间的关系为:c= (f﹣32),试分别求:(1)、当f=68和f=﹣4时,c的值;(2)、当c=10时,f的值.18. 若关于x,y的方程组 与 有相同的解.
(1)、求这个相同的解;(2)、求m,n的值.
19. 如图,A是∠MON边OM上一点,AE∥ON.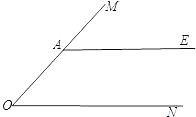 (1)、在图中作∠MON的角平分线OB,交AE于点B;(要求:尺规作图,保留作图痕迹,不写作法和证明)(2)、在(1)中,过点A画OB的垂线,垂足为点D,交ON于点C,连接CB,将图形补充完整,并证明四边形OABC是菱形.20. 在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:
(1)、在图中作∠MON的角平分线OB,交AE于点B;(要求:尺规作图,保留作图痕迹,不写作法和证明)(2)、在(1)中,过点A画OB的垂线,垂足为点D,交ON于点C,连接CB,将图形补充完整,并证明四边形OABC是菱形.20. 在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:该班学生参加各项服务的频数、频率统计表:
服务类别
频数
频率
文明宣传员
4
0.08
文明劝导员
10
义务小警卫
8
0.16
环境小卫士
0.32
小小活雷锋
12
0.24
请根据上面的统计图表,解答下列问题:
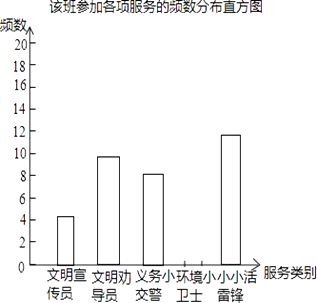 (1)、该班参加这次公益活动的学生共有名;(2)、请补全频数、频率统计表和频数分布直方图;(3)、若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.21. 如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3 ﹣3,CD∥AB,并与弧AB相交于点M、N.
(1)、该班参加这次公益活动的学生共有名;(2)、请补全频数、频率统计表和频数分布直方图;(3)、若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.21. 如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3 ﹣3,CD∥AB,并与弧AB相交于点M、N.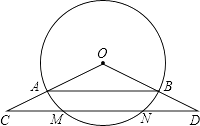 (1)、求线段OD的长;(2)、若sin∠C= ,求弦MN的长;(3)、在(2)的条件下,求优弧MEN的长度.22. 已知抛物线y=x2﹣2bx+c(1)、若抛物线的顶点坐标为(2,﹣3),求b,c的值;(2)、若b+c=0,是否存在实数x,使得相应的y的值为1,请说明理由;(3)、若c=b+2且抛物线在﹣2≤x≤2上的最小值是﹣3,求b的值.23. 如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2 , (这里规定:线段是面积为0的三角形)
(1)、求线段OD的长;(2)、若sin∠C= ,求弦MN的长;(3)、在(2)的条件下,求优弧MEN的长度.22. 已知抛物线y=x2﹣2bx+c(1)、若抛物线的顶点坐标为(2,﹣3),求b,c的值;(2)、若b+c=0,是否存在实数x,使得相应的y的值为1,请说明理由;(3)、若c=b+2且抛物线在﹣2≤x≤2上的最小值是﹣3,求b的值.23. 如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2 , (这里规定:线段是面积为0的三角形)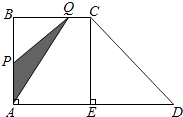
解答下列问题:
(1)、当x=2s时,y=cm2;当x= s时,y=cm2 .(2)、当5≤x≤14 时,求y与x之间的函数关系式.(3)、当动点P在线段BC上运动时,求出 S梯形ABCD时x的值.(4)、直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.