2017年四川省内江市资中县中考数学二模试卷

试卷更新日期：2017-06-29 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2017的倒数是（）

A、2017 B、﹣2017 C、 $\frac{1}{2017}$ D、﹣ $\frac{1}{2017}$

查看试题解析
2. 世界最大的500米口径球面射电望远镜（FAST）于2016年9月25日在贵州省平塘县落成启用，被誉为“中国天眼”，能够接收到137亿光年以外的电磁信号137亿用科学记数法表示为（）

A、137×10⁸ B、1.37×10⁹ C、1.37×10¹⁰ D、1.37×10¹¹

查看试题解析
3. 如图是由四个大小相同的正方体组成的几何体，那么它的主视图是（）

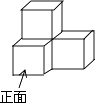A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、a⁶+a³=a⁹ B、a²•a³=a⁵ C、（2a）³=6a³ D、（a﹣b）²=a²﹣b²

查看试题解析
5. 如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为（）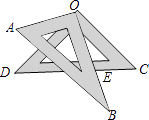

A、85° B、70° C、75° D、60°

查看试题解析
6. 若a＜b，则下列各式中，错误的是（）

A、a﹣3＜b﹣3 B、﹣a＜﹣b C、﹣2a＞﹣2b D、 $\frac{1}{3}$ a＜ $\frac{1}{3}$ b

查看试题解析
7. 数据3，6，7，4，x的平均数是5，则这组数据的中位数是（）

A、4 B、4.5 C、5 D、6

查看试题解析
8. 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂）是一次函数y=﹣ $\frac{1}{3}$ x+2图象上的两点，下列判断中，正确的是（）

A、y₁＞y₂ B、y₁＜y₂ C、当x₁＜x₂时，y₁＜y₂ D、当x₁＜x₂时，y₁＞y₂

查看试题解析
9. 如图，已知矩形ABCD中，R，P分别是DC、BC上的点，E，F分别是AP，RP的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（）

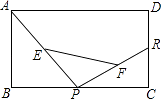A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不改变 D、线段EF的长不能确定

查看试题解析
10. 甲车行驶30千米与乙车行驶40千米所用时间相同，已知乙车每小时比甲车多行驶15千米，设甲车的速度为x千米/小时，依据题意列方程正确的是（）

A、 $\frac{30}{x} = \frac{40}{x - 15}$ B、 $\frac{30}{x - 15} = \frac{40}{x}$ C、 $\frac{30}{x} = \frac{40}{x + 15}$ D、 $\frac{30}{x + 15} = \frac{40}{x}$

查看试题解析
11. 计算机是将信息转换成二进制数进行处理的，二进制即“逢2进1”，如（1101）₂表示二进制数，将它转换成十进制形式是1×2³+1×2²+0×2¹+1×2⁰=13，那么将二进制（1111）₂转换成十进制形式是（）

A、8 B、15 C、30 D、31

查看试题解析
12. 如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S_△_ABC=S_四边形_AOCP ，其中正确的个数是（）

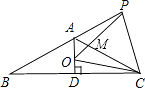A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 化简： $\frac{a}{a - b} + \frac{b}{b - a}$ = ．

查看试题解析
14. 分解因式：x³﹣4x= ．

查看试题解析
15. =在一个不透明的盒子中装有10个白球和若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出1个球，它恰好是白球的概率是 $\frac{2}{3}$ ，则该盒中黄球的个数为．

查看试题解析
16. 如图，在平面直角坐标系中有一正方形AOBC，反比例函数y= $\frac{k}{x}$ 经过正方形AOBC对角线的交点，半径为（6﹣3 $\sqrt{2}$ ）的圆内切于△ABC，则k的值为．

查看试题解析

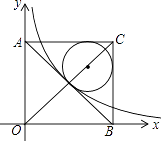
三、解答题

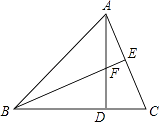
17. 计算：|1﹣ $\sqrt{2}$ |+（π﹣2014）⁰﹣2sin45°+（ $\frac{1}{2}$ ）^﹣² ．

查看试题解析
18. 如图，在△ABC中，∠ABC=45°，AD、BE是△ABC的高，AD、BE相交于点F．
求证：BF=AC．

查看试题解析
19.
“校园安全”受到全社会的广泛关注，东营市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如图两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：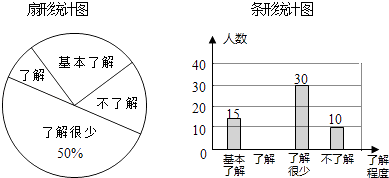

(1)、接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为；

(2)、请补全条形统计图；

(3)、若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；

(4)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

查看试题解析
20.
2016年11月3日，我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空，这标志着我国从航天大国迈向航天强国．如图，火箭从地面L处发射，当火箭到达A点时，从位于地面R处雷达站测得AR的距离是6km，仰角为42.4°；1秒后火箭到达B点，此时测得仰角为45.5°．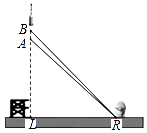

(1)、求发射台与雷达站之间的距离LR；

(2)、求这枚火箭从A到B的平均速度是多少？（结果精确到0.01，参考数据：sin42.4°≈0.67，cos42.4°≈0.74，tan42.4°≈0.905，sin45.5°≈0.71，cos45.5°≈0.70，tan45.5°≈1.02 ）

查看试题解析
21.
如图，在锐角△ABC中，BC=10，高AD=8，矩形EFPQ的一边QP在BC边上，E、F两点分别在AB、AC上，AD交EF于点H．

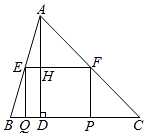(1)、求证： $\frac{A H}{A D}$ = $\frac{E F}{B C}$ ；

(2)、设EF的长为x．
①当x为何值时，矩形EFPQ为正方形？
②当x为何值时，矩形EFPQ的面积最大？并求其最大值．

查看试题解析

四、填空题

22. 已知 $\frac{3}{x}$ ﹣ $\frac{2}{y}$ =3，则 $\frac{4 x - x y - 6 y}{5 x y + 9 y - 6 x}$ = ．

查看试题解析
23. 如图，在反比例函数y= $\frac{10}{x}$ （x＞0）的图象上，有点P₁ ， P₂ ， P₃ ， P₄ ， …，它们的横坐标依次为2，4，6，8，…分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次记为S₁ ， S₂ ， S₃ ， …，S_n ，则S₁+S₂+S₃+…+S_n=（用含n的代数式表示）

查看试题解析
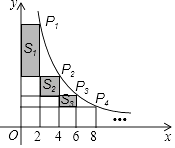24. 如图，△ABC中，∠C=90°，AC=6，AB=10，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则OD的长为．

查看试题解析
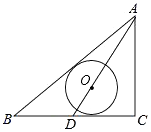25. 如图，在边长为4的菱形ABCD中，∠A=60°，M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则线段A′C长度的最小值是．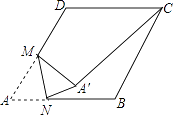

查看试题解析

五、解答题

26. 某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备，现要将这些设备全部运往A、B两市，其中运往A市18台、运往B市14台，从甲地运往A、B两市的费用分别为800元/台和500元/台，从乙地运往A、B两市的费用分别为700元/台和600元/台．设甲地运往A市的设备有x台．

(1)、请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数；

(2)、求出总运费y（元）与x（台）的函数关系式，并求出自变量的取值范围；

(3)、要使总运费不高于20200元，请你帮助该公司设计调配方案，并写出有哪几种方案，哪种方案总运费最小，最小值是多少？

查看试题解析
27.
如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．

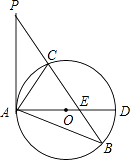(1)、求证：PA是⊙O的切线；

(2)、
过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长；

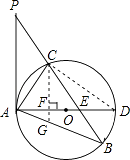(3)、在满足（2）的条件下，若AF：FD=1：2，GF=1，求⊙O的半径及sin∠ACE的值．

查看试题解析
28.
如图，抛物线y=ax²+bx+c（a≠0）与x轴、y轴分别交于A（﹣1，0）、B（3，0）、C（0，3）三点．

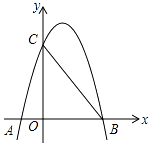(1)、试求抛物线的解析式；

(2)、P是直线BC上方抛物线上的一个动点，设P的横坐标为t，P到BC的距离为h，求h与t的函数关系式，并求出h的最大值．

(3)、设点M是x轴上的动点，在平面直角坐标系中，是否存在点N，使得以点A、C、M、N为顶点的四边形是菱形？若存在，求出所有符合条件的点N坐标；若不存在，说明理由．

查看试题解析