2017年上海市青浦区中考数学二模试卷
试卷更新日期:2017-06-29 类型:中考模拟
一、单项选择题
-
1. 下列运算中,正确的是( )A、2a﹣a=1 B、a+a=2a C、(a3)3=a6 D、a8÷a2=a42. 不等式组 的解集在数轴上可表示为( )A、
 B、
B、 C、
C、 D、
D、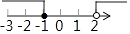 3. 二次根式 的值是( )A、﹣3 B、3或﹣3 C、9 D、34. 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
3. 二次根式 的值是( )A、﹣3 B、3或﹣3 C、9 D、34. 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( ) A、 B、 C、 D、15. 某集团公司有9个子公司,各个子公司所创年利润的情况如下表所示.各子公司所创年利润的众数和中位数分别是( )
A、 B、 C、 D、15. 某集团公司有9个子公司,各个子公司所创年利润的情况如下表所示.各子公司所创年利润的众数和中位数分别是( )年利润(千万元)
6
4
3
2
子公司个数
1
2
4
2
A、4千万元,3千万元 B、6千万元,4千万元 C、6千万元,3千万元 D、3千万元,3千万元6. 如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( ) A、
A、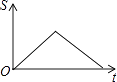 B、
B、 C、
C、 D、
D、
二、填空题
-
7. 若x:y=2:3,那么x:(x+y)= .8. 在实数范围内分解因式:x2﹣3= .9. =已知函数f(x)= ,那么f( ﹣1)= .10. 已知反比例函数y= 的图象经过一、三象限,则实数k的取值范围是 .11. 已知关于x的方程x2﹣2x+a=0有两个实数根,则实数a的取值范围是 .12. 方程 =1的解为 .13. 抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 .14. 布袋中装有3个红球和n个白球,它们除颜色外其它都相同,如果从布袋里随机摸出一个球,所摸到的球恰好是红球的概率是 ,那么布袋中白球有个.15. 化简:2 ﹣3( ﹣ )= .16. 如图,在菱形ABCD中,EF∥BC, = ,EF=3,则CD的长为 .
 17. 在△ABC中,已知BC=4cm,以边AC的中点P为圆心1cm为半径画⊙P,以边AB的中点Q为圆心x cm长为半径画⊙Q,如果⊙P与⊙Q相切,那么x=cm.18. 如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB.设BE=a,DC=b,那么AB= . (用含a、b的式子表示AB)
17. 在△ABC中,已知BC=4cm,以边AC的中点P为圆心1cm为半径画⊙P,以边AB的中点Q为圆心x cm长为半径画⊙Q,如果⊙P与⊙Q相切,那么x=cm.18. 如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB.设BE=a,DC=b,那么AB= . (用含a、b的式子表示AB)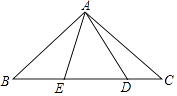
三、解答题:
-
19. 计算:20170+( )﹣1+6cos30°﹣|2﹣ |.20. 解方程: ﹣ =1﹣ .21. 已知直线y=﹣ x+3与x轴、y轴分别交于A、B两点,设O为坐标原点.(1)、求∠ABO的正切值;(2)、如果点A向左平移12个单位到点C,直线l过点C且与直线y=﹣ x+3平行,求直线l的解析式.22. 小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米, ≈1.732)
 23. 如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且 = ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
23. 如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且 = ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F. (1)、求证:PC=PE;(2)、当P是边AC的中点时,求证:四边形AECF是矩形.24. 已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
(1)、求证:PC=PE;(2)、当P是边AC的中点时,求证:四边形AECF是矩形.24. 已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.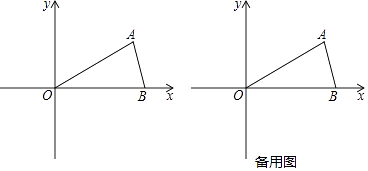 (1)、求点A、B的坐标;(2)、开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;(3)、设半径为2的⊙P与直线OA交于M、N两点,已知MN=2 ,P(m,2)(m>0),求m的值.25. 如图,△ABC的边AB是⊙O的直径,点C在⊙O上,已知AC=6cm,BC=8cm,点P、Q分别在边AB、BC上,且点P不与点A、B重合,BQ=k•AP(k>0),联接PC、PQ.
(1)、求点A、B的坐标;(2)、开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;(3)、设半径为2的⊙P与直线OA交于M、N两点,已知MN=2 ,P(m,2)(m>0),求m的值.25. 如图,△ABC的边AB是⊙O的直径,点C在⊙O上,已知AC=6cm,BC=8cm,点P、Q分别在边AB、BC上,且点P不与点A、B重合,BQ=k•AP(k>0),联接PC、PQ. (1)、求⊙O的半径长;(2)、当k=2时,设AP=x,△CPQ的面积为y,求y关于x的函数关系式,并写出定义域;(3)、如果△CPQ与△ABC相似,且∠ACB=∠CPQ,求k的值.
(1)、求⊙O的半径长;(2)、当k=2时,设AP=x,△CPQ的面积为y,求y关于x的函数关系式,并写出定义域;(3)、如果△CPQ与△ABC相似,且∠ACB=∠CPQ,求k的值.