2017年上海市普陀区中考数学二模试卷

试卷更新日期：2017-06-29 类型：中考模拟

进入出卷网下载

一、选择题：

1. 下列计算正确的是（）

A、a²•a³=a⁶ B、a³÷a³=a C、3a+3b=3ab D、（a³）²=a⁶

查看试题解析
2. 如果下列二次根式中有一个与 $\sqrt{a}$ 是同类二次根式，那么这个根式是（）

A、 $\sqrt{2}$ a B、 $\sqrt{3 a^{2}}$ C、 $\sqrt{a^{3}}$ D、 $\sqrt{a^{4}}$

查看试题解析
3. 在学校举办的“中华诗词大赛”中，有11名选手进入决赛，他们的决赛成绩各不相同，其中一名参赛选手想知道自己是否能进入前6名，他需要了解这11名学生成绩的（）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
4. 如图，在△ABC中，点D、E分别在边AB、AC上，如果∠A=50°，那么∠1+∠2的大小为（）

A、130° B、180° C、230° D、260°

查看试题解析
5.
如图，在△ABC中，中线AD、CE交于点O，设 $\vec{A B}$ = $\vec{a}$ ， $\vec{B C}$ = $\vec{b}$ ，那么向量 $\vec{A O}$ 用向量 $\vec{a}$ 、 $\vec{b}$ 表示为（）

A、 $\vec{a}$ + $\frac{1}{2} \vec{b}$ B、 $\frac{2}{3} \vec{a}$ + $\frac{1}{3} \vec{b}$ C、 $\frac{2}{3} \vec{a}$ + $\frac{2}{3} \vec{b}$ D、 $\frac{1}{2} \vec{a}$ + $\frac{1}{4} \vec{b}$

查看试题解析
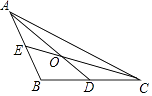6. 在△ABC中，AB=AC=6，cos∠B= $\frac{2}{3}$ ，以点B为圆心，AB为半径作圆B，以点C为圆心，半径长为13作圆C，圆B与圆C的位置关系是（）

A、外切 B、相交 C、内切 D、内含

查看试题解析

二、填空题：

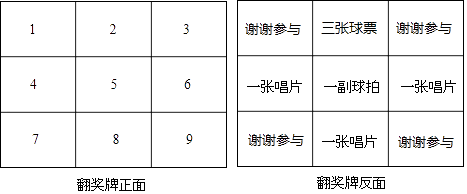
7. 分解因式：a³﹣4a= ．

查看试题解析
8. 方程x= $\sqrt{4 - 3 x}$ 的根是．

查看试题解析
9. 不等式组 ${\begin{matrix} 2 x - 3 < 0 \\ 3 x \geq 0 \end{matrix}$ 的解集是．

查看试题解析
10. 函数y= $\frac{1}{\sqrt[3]{x - 5}}$ 的定义域是．

查看试题解析
11. 如果关于x的方程x²﹣3x+m=0没有实数根，那么m的取值范围是．

查看试题解析
12. 已知反比例函数y= $\frac{k}{x}$ （k是常数，k≠0）的图象在第二、四象限，点A（x₁ ， y₁）和点B（x₂ ， y₂）在函数的图象上，当x₁＜x₂＜0时，可得y₁y₂ ．（填“＞”、“=”、“＜”）．

查看试题解析
13. 一次抽奖活动设置了翻奖牌（图展示的分别是翻奖牌的正反两面），抽奖时，你只能看到正面，你可以在9个数字中任意选中一个数字，可见抽中一副球拍的概率是 $\frac{1}{9}$ ，那么请你根据题意写出一个事件，使这个事件发生的概率是 $\frac{1}{3}$ ．这个事件是．

查看试题解析
14. 正八边形的中心角等于度．

查看试题解析
15. 如图，在△ABC中，D、E分别是边AB、AC上的点，如果 $\frac{A D}{D B}$ = $\frac{A E}{E C}$ = $\frac{1}{2}$ ，那么△ADE与△ABC周长的比是．

查看试题解析
16. 某班学生参加环保知识竞赛，已知竞赛得分都是整数．把参赛学生的成绩整理后分为6小组，画出竞赛成绩的频数分布直方图（如图所示），根据图中的信息，可得成绩高于60分的学生占全班参赛人数的百分率是．

查看试题解析
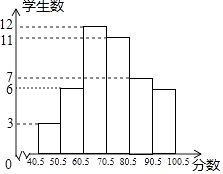17. 一个滑轮起重装置如图所示，滑轮的半径是10cm，当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时，重物上升 cm（结果保留π）．

查看试题解析
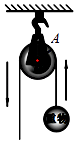18. 如图，将△ABC绕点B按逆时针方向旋转得到△EBD，点E、点D分别与点A、点C对应，且点D在边AC上，边DE交边AB于点F，△BDC∽△ABC．已知BC= $\sqrt{10}$ ，AC=5，那么△DBF的面积等于．

查看试题解析

三、解答题：

19. 计算：（ $\frac{1}{2}$ ）^﹣³+（﹣1）²⁰¹⁷+ $\frac{1}{2 - \sqrt{3}}$ ﹣3sin60°．

查看试题解析
20. 解方程组： ${\begin{matrix} x - 3 y + 2 = 0 \\ x^{2} + 4 x y + 4 y^{2} = 9 \end{matrix}$ ．

查看试题解析
21. 在平面直角坐标系xOy中，已知正比例函数的图象与反比例函数y= $\frac{8}{x}$ 的图象交于点A（m，4）．

(1)、求正比例函数的解析式；

(2)、将正比例函数的图象向下平移6个单位得到直线l，设直线l与x轴的交点为B，求∠ABO的正弦值．

查看试题解析
22. 上海首条中运量公交线路71路已正式开通．该线路西起沪青平公路申昆路，东至延安东路中山东一路，全长17.5千米.71路车行驶于专设的公交车道，又配以专用的公交信号灯．经测试，早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米，因此单程可节省时间22.5分钟．求早晚高峰时段71路车在专用车道内行驶的平均车速．

查看试题解析
23. 已知：如图，在平行四边形ABCD中，AC为对角线，E是边AD上一点，BE⊥AC交AC于点F，BE、CD的延长线交于点G，且∠ABE=∠CAD．

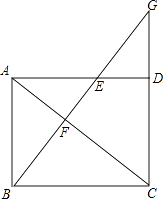(1)、求证：四边形ABCD是矩形；

(2)、如果AE=EG，求证：AC²=BC•BG．

查看试题解析
24.
如图，在平面直角坐标系xOy中，二次函数y=x²﹣2x+m（m＞0）的对称轴与比例系数为5的反比例函数图象交于点A，与x轴交于点B，抛物线的图象与y轴交于点C，且OC=3OB．

(1)、求点A的坐标；

(2)、求直线AC的表达式；

(3)、点E是直线AC上一动点，点F在x轴上方的平面内，且使以A、B、E、F为顶点的四边形是菱形，直接写出点F的坐标．

查看试题解析
25. 如图，半圆O的直径AB=10，有一条定长为6的动弦CD在弧AB上滑动（点C、点D分别不与点A、点B重合），点E、F在AB上，EC⊥CD，FD⊥CD．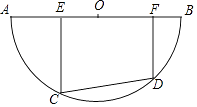

(1)、求证：EO=OF；

(2)、联结OC，如果△ECO中有一个内角等于45°，求线段EF的长；

(3)、当动弦CD在弧AB上滑动时，设变量CE=x，四边形CDFE面积为S，周长为l，问：S与l是否分别随着x的变化而变化？试用所学的函数知识直接写出它们的函数解析式及函数定义域，以说明你的结论．

查看试题解析