2017年山东省泰安市中考数学一模试卷
试卷更新日期:2017-06-29 类型:中考模拟
一、选择题
-
1. ﹣2的绝对值是( )A、﹣ B、 C、2 D、﹣22. 下列运算正确的是( )A、x3•x2=x5 B、(x3)3=x6 C、x5+x5=x10 D、x6﹣x3=x33. 不等式组 的整数解是( )A、﹣1,0 B、﹣1,1 C、0,1 D、﹣1,0,14. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 一个几何体的主视图和俯视图如图所示,那么它的左视图可能是( )
5. 一个几何体的主视图和俯视图如图所示,那么它的左视图可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 化简:(1+ )÷ 结果为( )A、4x B、3x C、2x D、x7. 苏州市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽一棵,则树苗正好用完.设原有树苗a棵,则根据题意列出方程正确的是( )A、5(a+21﹣1)=6(a﹣1) B、5(a+21)=6(a﹣1) C、5(a+21)﹣1=6a D、5(a+21)=6a8. 暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( )A、 B、 C、 D、9. 芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为( )A、2.01×10﹣6千克 B、0.201×10﹣5千克 C、20.1×10﹣7千克 D、2.01×10﹣7千克10. 在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
6. 化简:(1+ )÷ 结果为( )A、4x B、3x C、2x D、x7. 苏州市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽一棵,则树苗正好用完.设原有树苗a棵,则根据题意列出方程正确的是( )A、5(a+21﹣1)=6(a﹣1) B、5(a+21)=6(a﹣1) C、5(a+21)﹣1=6a D、5(a+21)=6a8. 暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( )A、 B、 C、 D、9. 芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为( )A、2.01×10﹣6千克 B、0.201×10﹣5千克 C、20.1×10﹣7千克 D、2.01×10﹣7千克10. 在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
人数
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数分别是( )
A、1.70,1.65 B、1.70,1.70 C、1.65,1.70 D、3,411. 如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连接AC′交A′C于D,则△C′DC的面积为( ) A、10 B、8 C、6 D、412. 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y= (x>0)上,则k的值为( )
A、10 B、8 C、6 D、412. 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y= (x>0)上,则k的值为( )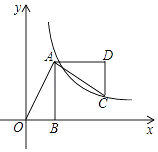 A、2 B、3 C、4 D、613. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分的面积为( )
A、2 B、3 C、4 D、613. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分的面积为( )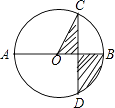 A、2π B、π C、 D、14. 如图,点A、B、C都在⊙O上,点B为弧AC的中点,若∠AOB=72°,则∠OAC的度数是( )
A、2π B、π C、 D、14. 如图,点A、B、C都在⊙O上,点B为弧AC的中点,若∠AOB=72°,则∠OAC的度数是( ) A、18° B、30° C、36° D、72°15. 在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、
A、18° B、30° C、36° D、72°15. 在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、 B、
B、 C、
C、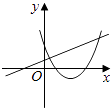 D、
D、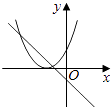 16. 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
16. 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )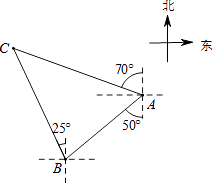 A、10 海里 B、10 海里 C、10 海里 D、20 海里17. 在矩形ABCD中,AB=1,AD= ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( )
A、10 海里 B、10 海里 C、10 海里 D、20 海里17. 在矩形ABCD中,AB=1,AD= ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( ) A、1 B、2 C、3 D、418. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( )
A、1 B、2 C、3 D、418. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( ) A、 B、 C、 D、19. 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).下列结论:
A、 B、 C、 D、19. 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).下列结论:①ac<0;
②4a﹣2b+c>0;
③抛物线与x轴的另一个交点是(4,0);
④点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2 . 其中正确的个数为( )
 A、1 B、2 C、3 D、420.
A、1 B、2 C、3 D、420.矩形ABCD中,AD=8cm,AB=6cm,动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动,E点运动到B点停止,F点继续运动,运动到点D停止.如图可得到矩形CFHE,设F点运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是如图中的( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
21. 分解因式:m3﹣4m2+4m= .22. 分式方程 的解为 .23. 如图所示,PA、PB切⊙O于点A、B,连接AB交直线OP于点C,若⊙O的半径为3,PA=4,则OC的长为 .
 24. 如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在y轴上,点O,B1 , B2 , B3…都在直线l上,则点B2017的坐标是 .
24. 如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在y轴上,点O,B1 , B2 , B3…都在直线l上,则点B2017的坐标是 .
三、解答题
-
25. 学校准备购置甲乙两种羽毛球拍若干,已知甲种球拍的单价比乙种球拍的单价多40元,且购买4副甲种球拍与购买6副乙种球拍的费用相同.(1)、两种球拍的单价各是多少元?(2)、若学校准备购买100副甲乙两种羽毛球拍,且购买甲种球拍的费用不少于乙种球拍费用的3倍,问购买多少副甲种球拍总费用最低?26. 如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y= (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
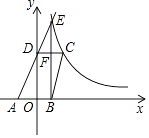 (1)、若EB= OD,求点E的坐标;(2)、若四边形ABCD为平行四边形,求过A、D两点的函数关系式.27. 如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB,
(1)、若EB= OD,求点E的坐标;(2)、若四边形ABCD为平行四边形,求过A、D两点的函数关系式.27. 如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB, (1)、求证:AG=DF;(2)、过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二
(1)、求证:AG=DF;(2)、过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二
找出图中与AB相等的线段,并证明.
28. △ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.(1)、如图1,
求证:DE•CD=DF•BE
(2)、D为BC中点如图2,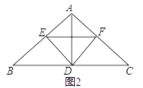
连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及 的值.
29. 如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.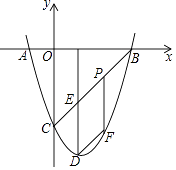 (1)、求出抛物线y=x2+bx+c的表达式;(2)、连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
(1)、求出抛物线y=x2+bx+c的表达式;(2)、连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.