2017年山东省青岛市市北区中考数学一模试卷

试卷更新日期：2017-06-29 类型：中考模拟

进入出卷网下载

一、选择题

1. 相反数是5的数是（）

A、5 B、﹣5 C、 $\frac{1}{5}$ D、﹣ $\frac{1}{5}$

查看试题解析
2. 下列图形既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3.
图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①②③④某一位置，所组成的图形不能围成正方体的位置是（）

A、① B、② C、③ D、④

查看试题解析
4.
线段MN在直角坐标系中的位置如图所示，将MN绕点M逆时针旋转90°得到线段M₁N₁ ，则点N的对应点N₁的坐标为（）

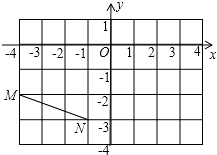A、（0，0） B、（﹣5，﹣4） C、（﹣3，1） D、（﹣1，﹣3）

查看试题解析
5. 根据表格估计一元二次方程x²+2x﹣4=0的一个解的范围在（）
x
﹣1
0
1
2
3
x²+2x﹣4
﹣5
﹣4
﹣1
4
11

A、﹣1＜x＜0 B、0＜x＜1 C、1＜x＜2 D、2＜x＜3

查看试题解析
6. 如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P=40°，则∠ABC的度数为（）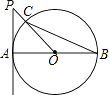

A、20° B、25° C、40° D、50°

查看试题解析
7. 八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍．设骑车学生的速度为x千米/小时，则所列方程正确的是（）

A、 $\frac{10}{x}$ ﹣ $\frac{10}{2 x}$ =20 B、 $\frac{10}{2 x}$ ﹣ $\frac{10}{x}$ =20 C、 $\frac{10}{x}$ ﹣ $\frac{10}{2 x}$ = $\frac{1}{3}$ D、 $\frac{10}{2 x}$ ﹣ $\frac{10}{x}$ = $\frac{1}{3}$

查看试题解析
8. 如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S_△_AOE：S_四边形_DGOF=2：7．其中正确结论的个数是（）

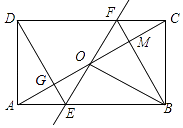A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

9. 计算： $\frac{\sqrt{48} - \sqrt{3}}{\sqrt{12}}$ = ．

查看试题解析
10. 某种细胞的直径是0.00000095米，将0.00000095米用科学记数法表示为．

查看试题解析
11. 某学校要从甲、乙两支女生礼仪队中，选拔一支身高相对整齐的队伍，代表学校承接迎宾任务，对两队女生升高情况（cm）的统计分析如表所示，在其它各项指标都相同的情况下，你认为队（填甲或乙）会被录取，理由是．

平均数
标准差
中位数
甲队
1.72
0.038
1.73
乙队
1.69
0.025
1.70

查看试题解析
12. 某产品每件成本10元，试销阶段每件产品的销售单价x（元/件）与日销售量y（件）之间的关系如下表．
x（元∕件）
15
18
20
22
…
y（件）
250
220
200
180
…
按照这样的规律可得，日销售利润w（元）与销售单价x（元/件）之间的函数关系式是．

查看试题解析
13. 如图，一根5m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A（羊只能在草地上活动），那么小羊A在草地上的最大活动区域面积是平方米．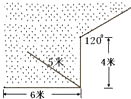

查看试题解析
14.
如图所示，已知点C（1，0），直线y=﹣x+7与两坐标轴分别交于A，B两点，D，E分别是AB，OA上的动点，则△CDE周长的最小值是．

查看试题解析

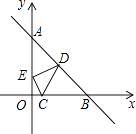
三、解答题

15.
用圆规、直尺作图，不写作法，但到保留作图痕迹．
已知：线段a，
求作：正方形ABCD，使其对角线AC=a．

查看试题解析
16. 计算题

(1)、化简：（ $\frac{a^{2}}{a - 3}$ + $\frac{9}{3 - a}$ ）÷ $\frac{a + 3}{a}$

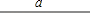(2)、解不等式组 ${\begin{matrix} 2 x + 1 > 0 ① \\ \frac{2 - x}{2} \geq \frac{x + 3}{3} ② \end{matrix}$ ．

查看试题解析
17. 甲、乙两个人做游戏：在一个不透明的口袋中装有4张相同的纸牌，它们分别标有数字1，2，3，4．从中随机摸出一张纸牌然后放回，再随机摸出一张纸牌，若两次摸出的纸牌上数字之和是3的倍数，则甲胜；否则乙胜．这个游戏对双方公平吗？请列表格或画树状图说明理由．

查看试题解析
18.
如图，某校教学楼AB的后面有一建筑物CD，在距离CD的正后方30米的观测点P处，以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A，而在建筑物CD上距离地面3米高的E处，测得教学楼的顶端A的仰角为45°，求教学楼AB的高度．
（参考数据：sin22°≈ $\frac{3}{8}$ ，cos22°≈ $\frac{15}{16}$ ，tan22°≈ $\frac{2}{5}$ ）

查看试题解析
19. 中华文明，源远流长；中华诗词，寓意深广．为了传承优秀传统文化，我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次海选比赛的成绩分布情况，随机抽取了其中200名学生的海选比赛成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列统计图表：
抽取的200名学生海选成绩分组表
组别
海选成绩x
A组
50≤x＜60
B组
60≤x＜70
C组
70≤x＜80
D组
80≤x＜90
E组
90≤x＜100
请根据所给信息，解答下列问题：

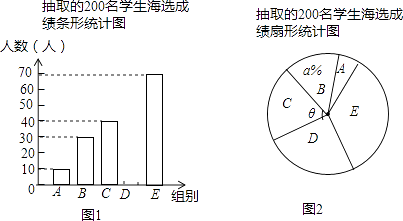(1)、请把图1中的条形统计图补充完整；（温馨提示：请画在答题卷相对应的图上）

(2)、在图2的扇形统计图中，记表示B组人数所占的百分比为a%，则a的值为，表示C组扇形的圆心角θ的度数为度；

(3)、规定海选成绩在90分以上（包括90分）记为“优等”，请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人？

查看试题解析
20. 如图，在平面直角坐标系xOy中，一次函数y₁=ax+b（a，b为常数，且a≠0）与反比例函数y₂= $\frac{m}{x}$ （m为常数，且m≠0）的图象交于点A（﹣2，1）、B（1，n）

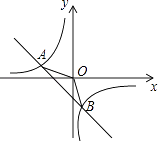(1)、求反比例函数与一次函数的解析式；

(2)、连接OA、OB，求△AOB的面积；

(3)、直接写出当y₁＜y₂时，自变量x的取值范围．

查看试题解析
21. 如图，在△ABC中，BD平分∠ABC，AE⊥BD于点O，交BC于点E，AD∥BC，连接CD．

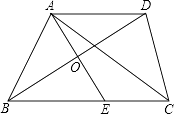(1)、求证：AO=EO；

(2)、若AE是△ABC的中线，则四边形AECD是什么特殊四边形？证明你的结论．

查看试题解析
22. 如图，需在一面墙上绘制两个形状相同的抛物绒型图案，按照图中的直角坐标系，最高点M到横轴的距离是4米，到纵轴的距离是6米；纵轴上的点A到横轴的距离是1米，右侧抛物线的最大高度是左侧抛物线最大高度的一半．（结果保留整数或分数，参考数据： $\sqrt{3}$ = $\frac{7}{4}$ ， $\sqrt{6}$ = $\frac{5}{2}$ ）

(1)、求左侧抛物线的表达式；

(2)、求右侧抛物线的表达式；

(3)、求这个图案在水平方向上的最大跨度是多少米．

查看试题解析
23.
探究题

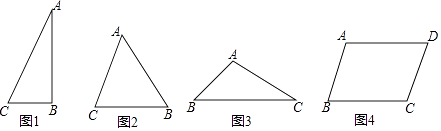
【问题提出】
已知任意三角形的两边及夹角（是锐角），求三角形的面积．
【问题探究】
为了解决上述问题，让我们从特殊到一般展开探究．
探究：在Rt△ABC（图1）中，∠ABC=90°，AC=b，BC=a，∠C=α，求△ABC的面积（用含a、b、α的代数式表示）
在Rt△ABC中，∠ABC=90°
∴sinα= $\frac{A B}{A C}$
∴AB=b•sinα
∴S_△_ABC= $\frac{1}{2}$ BC•AB= $\frac{1}{2}$ absinα

(1)、探究一：
锐角△ABC（图2）中，AC=b，BC=a，∠C=α（0°＜α＜90°）
求：△ABC的面积．（用含a、b、α的代数式表示）

(2)、探究二：
钝角△ABC（图3）中，AC=b，BC=a，∠C=α（0°＜α＜90°）
求：△ABC的面积．（用含a、b、α的代数式表示）

(3)、【问题解决】
用文字叙述：已知任意三角形的两边及夹角（是锐角），求三角形面积的方法
是

(4)、已知平行四边形ABCD（图4）中，AB=b，BC=a，∠B=α（0°＜α＜90°）
求：平行四边形ABCD的面积．（用含a、b、α的代数式表示）

查看试题解析
24.
已知：如图，菱形ABCD中，AB=10cm，BD=12cm，对角线AC与BD相交于点O，直线MN以1cm/s从点D出发，沿DB方向匀速运动，运动过程中始终保持MN⊥BD，垂足是点P，过点P作PQ⊥BC，交BC于点Q．（0＜t＜6）

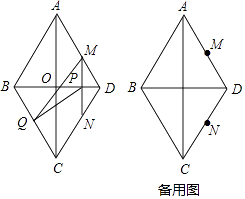(1)、求线段PQ的长；（用含t的代数式表示）

(2)、设△MQP的面积为y（单位：cm²），求y与t的函数关系式；

(3)、是否存在某时刻t，使线段MQ恰好经过点O？若存在求出此时t的值；若不存在，请说明理由．

查看试题解析

	平均数	标准差	中位数
甲队	1.72	0.038	1.73
乙队	1.69	0.025	1.70

组别	海选成绩x
A组	50≤x＜60
B组	60≤x＜70
C组	70≤x＜80
D组	80≤x＜90
E组	90≤x＜100

x	﹣1	0	1	2	3
x²+2x﹣4	﹣5	﹣4	﹣1	4	11

x（元∕件）	15	18	20	22	…
y（件）	250	220	200	180	…