2017年江苏省无锡市新吴区中考数学一模试卷

试卷更新日期：2017-06-29 类型：中考模拟

进入出卷网下载

一、选择题

1. $\frac{1}{4}$ 的相反数等于（）

A、 $- \frac{1}{4}$ B、4 C、 $\frac{1}{4}$ D、± $\frac{1}{4}$

查看试题解析
2. 下列运算正确的是（）

A、a²•a³=a⁶ B、（﹣y²）³=y⁶ C、（m²n）³=m⁵n³ D、﹣2x²+5x²=3x²

查看试题解析
3. 下列图形中，中心对称图形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列事件中，是确定事件的是（）

A、明天太阳从东方升起 B、打开电视机正在播放动画片 C、篮球运动员身高都在2米以上 D、抛一枚硬币，正面向上

查看试题解析
5. 如图，数轴上A，B两点分别对应实数a，b，则下列结论正确的是（）

A、a+b＞0 B、ab＞0 C、a﹣b＞0 D、|a|﹣|b|＞0

查看试题解析
6. 如图，在四边形ABCD中，AD∥BC，要是四边形ABCD成为平行四边形，则应增加的条件是（）

A、AB=CD B、∠BAD=∠DCB C、AC=BD D、∠ABC+∠BAD=180°

查看试题解析
7. 某校九年级（1）班全体学生2016年初中毕业体育考试的成绩统计如下表：
成绩（分）
24
25
26
27
28
29
30
人数（人）
2
5
6
6
8
7
6
根据上表中的信息判断，下列结论中错误的是（）

A、该班一共有40名同学 B、该班学生这次考试成绩的众数是28分 C、该班学生这次考试成绩的中位数是28分 D、该班学生这次考试成绩的平均数是28分

查看试题解析
8. 如果一个等腰三角形的两边长分别为方程x²﹣5x+4=0的两根，则这个等腰三角形的周长为（）

A、6 B、9 C、6或9 D、以上都不正确

查看试题解析
9. 如图，如果从半径为9cm的圆形纸片剪去 $\frac{1}{3}$ 圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（）

A、6cm B、 $3 \sqrt{5}$ cm C、8cm D、 $5 \sqrt{3}$ cm

查看试题解析
10. 如图，矩形ABCD中，AB=6cm，AD=4cm，点M是边AB的中点，点P是矩形边上的一个动点，点P从M出发在矩形的边上沿着逆时针方向运动，则当点P沿着矩形的边逆时针旋转一周时，△DMP面积刚好为5cm²的时刻有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 若 $\sqrt{3 x - 6}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 无锡阳山，风景如画，粉红的桃花，洁白的梨花，金灿灿的油菜花，引得众多游客流连忘返，据统计今年清明小长假前往阳山踏青赏花游客超过130000人次，把130000用科学记数法表示为．

查看试题解析
13. 分解因式：4a²﹣b²= ．

查看试题解析
14. 反比例函数的图象经过点（﹣1，2），图象上有两个点的坐标为（﹣1，y₁），（﹣2，y₂），则y₁与y₂的大小关系为．

查看试题解析
15. 如图，已知AB是⊙O的直径，BC为弦，过圆心O作OD⊥BC交弧BC于点D，连接DC，若∠DCB=32°，则∠BAC= ．

查看试题解析
16. 已知直角平面坐标系内有两点，点P（4，2）与点Q（a，a+2），则PQ的最小值为．

查看试题解析
17. 如图，在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB₁E，则△AB₁E与四边形AECD重叠部分的面积是．

查看试题解析
18. 点B（a，5）在第二象限，点C在y轴上移动，以BC为斜边作等腰直角△BCD，我们发现直角顶点D点随着C点的移动也在一条直线上移动，这条直线的函数表达式是．

查看试题解析

三、解答题

19. 计算下面各题

(1)、计算： $\sqrt{8}$ +（2011﹣ $\sqrt{3}$ ）⁰﹣（ $\frac{1}{2}$ ）^﹣¹

(2)、计算：（ $\frac{1}{x - y}$ + $\frac{1}{x + y}$ ）÷ $\frac{2 x}{x^{2} + 2 x y + y^{2}}$ ．

查看试题解析
20. 解下列各题

(1)、解方程： $\frac{2 - x}{x - 3}$ =1﹣ $\frac{1}{3 - x}$

(2)、解不等式组： ${\begin{matrix} 2 x - 1 \leq 2 \\ \frac{x - 1}{4} < \frac{x}{3} \end{matrix}$ ．

查看试题解析
21. 如图所示，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．

(1)、填空：∠ABC= ， BC=；

(2)、判断△ABC与△DEF是否相似？并证明你的结论．

查看试题解析
22. 如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1，2，3，4四个数字）．游戏规则是游戏者每掷一次骰子，棋子按着地一面所示的数字前进相应的格数．例如：若棋子位于A处，游戏者所掷骰子着地一面所示数字为3，则棋子由A处前进3个方格到达B处．请用画树形图法（或列表法）求掷骰子两次后，棋子恰好由A处前进6个方格到达C处的概率．

查看试题解析
23. 某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为A，B，C，D四类，其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表：
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06

(1)、表中的a= ， b=；

(2)、根据表中数据，求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数；

(3)、若该校有学生1000名，根据调查结果估计该校学生中类别为D的人数约为多少？

查看试题解析
24. 如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC．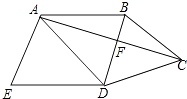

(1)、求证：四边形ABDE是平行四边形；

(2)、如果DA平分∠BDE，AB=5，AD=6，求AC的长．

查看试题解析
25. 如图，点P是等边三角形ABC内部一个动点，∠APB=120°，⊙O是△APB的外接圆．AP，BP的延长线分别交BC，AC于D，E．

(1)、求证：CA，CB是⊙O的切线；

(2)、已知AB=6，G在BC上，BG=2，当PG取得最小值时，求PG的长及∠BGP的度数．

查看试题解析
26. 虽然近几年无锡市政府加大了太湖水治污力度，但由于大规模、高强度的经济活动和日益增加的污染负荷，使部分太湖水域水质恶化，富营养化不断加剧．为了保护水资源，我市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：
月用水量（吨）
单价（元/吨）
不大于10吨部分
1.5
大于10吨不大于m吨部分（20≤m≤50）
2
大于m吨部分
3

(1)、若某用户六月份用水量为18吨，求其应缴纳的水费；

(2)、记该用户六月份用水量为x吨，缴纳水费为y元，试列出y关于x的函数关系式；

(3)、若该用户六月份用水量为40吨，缴纳水费y元的取值范围为70≤y≤90，试求m的取值范围．

查看试题解析
27.
如图，A（0，2），B（1，0），点C为线段AB的中点，将线段BA绕点B按顺时针方向旋转90°得到线段BD，抛物线y=ax²+bx+c（a≠0）经过点D．

(1)、若该抛物线经过原点O，且a=﹣ $\frac{1}{3}$ ，求该抛物线的解析式；

(2)、在（1）的条件下，点P（m，n）在抛物线上，且∠POB锐角，满足∠POB+∠BCD＜90°，求m的取值范围．

查看试题解析
28. 解答题

(1)、
如图1，已知△ABC，以AB，AC为边分别向△ABC外作等边△ABD和等边△ACE，连结BE，CD，请你完成图形（尺规作图，不写作法，保留作图痕迹），并证明：BE=CD；

(2)、
如图2，利用（1）中的方法解决如下问题：在四边形ABCD中，AD=3，CD=2，∠ABC=∠ACB=∠ADC=45°，求BD的长．

(3)、
如图3，四边形ABCD中，∠CAB=90°，∠ADC=∠ACB=α，tanα= $\frac{4}{3}$ ，CD=5，AD=12，求BD的长．

查看试题解析

月用水量（吨）	单价（元/吨）
不大于10吨部分	1.5
大于10吨不大于m吨部分（20≤m≤50）	2
大于m吨部分	3

成绩（分）	24	25	26	27	28	29	30
人数（人）	2	5	6	6	8	7	6

类别	A	B	C	D
频数	30	40	24	b
频率	a	0.4	0.24	0.06