2017年江苏省泰州市海陵区中考数学一模试卷

试卷更新日期：2017-06-29 类型：中考模拟

进入出卷网下载

一、选择题

1. 在﹣5，0，﹣3，6这四个数中，绝对值最小的数是（）

A、﹣3 B、0 C、﹣5 D、6

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{{(- 5)}^{2}}$ =﹣5 B、（x³）²=x⁵ C、x⁶÷x³=x² D、（ $\frac{1}{2}$ ）^﹣²=4

查看试题解析
3. 已知x=2是方程x²+bx﹣2=0的一个根，则b的值是（）

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
4. 如图，将一张锐角三角形纸片沿中位线剪开，拼成一个新的图形，这个新的图形一定是下列图形中的（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
5. 如图是一个由几个同样的立方体叠成的几何体，则这一几何体的三视图中，既是轴对称图形又是中心对称图形的是（）

A、主视图和俯视图 B、俯视图 C、俯视图和左视图 D、主视图

查看试题解析
6. 如图，抛物线y=ax²+bx+c（a≠0）过点（1，0）和点（0，﹣1），且顶点在第三象限，则a的取值范围是（）

A、a＞0 B、0＜a＜1 C、1＜a＜2 D、﹣1＜a＜1

查看试题解析

二、填空题

7. 计算： $- \sqrt{25}$ = ．

查看试题解析
8. 因式分解：ab²﹣9a= ．

查看试题解析
9. 数据1、0、2、3、x的平均数是2，x= ．

查看试题解析
10. 2016年泰州市全市地区生产总值约为4100亿元，这个数据用科学记数法可表示为元．

查看试题解析
11. 直线y=kx+b如图，则关于x的不等式kx+b≤﹣2的解集是．

查看试题解析
12. 如图，在边长为3cm的正方形ABCD中，点E为BC边上的任意一点，AF⊥AE，AF交CD的延长线于F，则四边形AFCE的面积为 cm² ．

查看试题解析
13. 如图，CD是⊙O的直径，弦AB⊥CD于点H，若∠D=30°，CH=1cm，则AB=cm．

查看试题解析
14. 一个圆锥的母线和底面直径都为2，则圆锥的侧面积为．

查看试题解析
15.
如图，点B在x的正半轴上，且BA⊥OB于点B，将线段BA绕点B逆时针旋转60°到BB′的位置，且点B′的坐标为（1， $\sqrt{3}$ ）．若反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过A点，则k= ．

查看试题解析
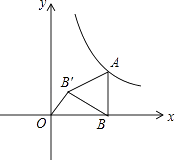16. 如图，射线OP过Rt△ABC的边AC、AB的中点M、N，AC=4cm，BC=4 $\sqrt{3}$ cm，OM=3cm．射线OP上有一动点Q从点O出发，沿射线OP以每秒1cm的速度向右移动，以Q为圆心，QM为半径的圆，经过t秒与BC、AB中的一边所在的直线相切，请写出t的所有可能值（单位：秒）

查看试题解析

三、解答题

17. 计算或化简：

(1)、2cos30°﹣ $\frac{3}{\sqrt{3}}$ +（ $\frac{1}{3}$ ）⁰+（﹣1）²⁰¹⁷

(2)、（1+ $\frac{1}{m}$ ）÷ $\frac{m^{2} - 1}{m^{2} - 2 m + 1}$ ．

查看试题解析
18. 已知关于x的一元二次方程x²+5x+3﹣3m=0有两个不相等的实数根．

(1)、求m的取值范围；

(2)、若m为负整数，求此时方程的根．

查看试题解析
19. 如图，已知点M、N分别为▱ABCD的边CD、AB的中点，连接AM、CN．

(1)、证明：AM=CN；

(2)、过点B作BH⊥AM于点H，交CN于点E，连接CH，判断线段CB、CH的数量关系，并说明理由．

查看试题解析
20. 在全民创业的热潮中，小王研制并投产了一种新产品，每件制造成本为9元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y=﹣x+25．（利润=售价﹣制造成本）

(1)、写出每月的利润W（万元）与销售单价x（元）之间的函数关系式；

(2)、当销售单价为多少元时，厂商每月获得的利润为55万元？

(3)、当销售单价为多少元时，厂商每月获得的利润最大？最大利润为多少万元？

查看试题解析
21. “3.15“植树节活动后，某校对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测，以下是根据观测数据制成的统计图表的一部分；
表1：栽下的各品种树苗棵数统计表表
植树品种
甲种
乙种
丙种
丁种
植树棵数
150
125
125
请你根据以上信息解答下列问题：

(1)、这次栽下的四个品种的树苗共棵，乙品种树苗棵．

(2)、图1中，甲 %、乙 %；

(3)、已知这批树苗成活率为90%，将图2补充完整．

查看试题解析
22. 有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B 布袋中有三个完全相同的小球，分别标有数字﹣1，﹣2和﹣3．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y）．

(1)、用列表或画树状图的方法写出点Q的所有可能坐标；

(2)、求点Q落在直线y=﹣x﹣1上的概率．

查看试题解析
23.
某兴趣小组想测量位于一池塘两端的A、B之间的距离，组长小明带领小组成员沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到达点D处，测得∠BDF=60°，已知AB与EF之间的距离为60米，求A、B两点的距离．

查看试题解析
24. 如图，AB是⊙O的直径，BC交⊙O于点D，E是BD弧上的一点，OE⊥BD于点G，连接AE交BC于点F，AC是⊙O的切线．

(1)、求证：∠ACB=2∠EAB；

(2)、若cos∠ACB= $\frac{2}{5}$ ，AC=10，求BF的长．

查看试题解析
25.
如图，平面直角坐标系xOy中，一次函数y=﹣x+b（b为常数，b＞0）的图象与x轴、y轴分别交于A、B两点，半径为5的圆⊙O与x轴正半轴相交于点C，与y轴相交于D、E两点．

(1)、若直线AB交劣弧 $\hat{C D}$ 于P、Q两点（异于C、D）
①当P点坐标为（3，4）时，求b值；
②求∠CPE的度数，并用含b的代数式表示弦PQ的长（写出b的取值范围）；

(2)、当b=6时，线段AB上存在几个点F，使∠CFE=45°？请说明理由．

查看试题解析
26.
如图，在平面直角坐标系中，四边形ABCO为正方形，A点坐标为（0，2），点P为x轴负半轴上一动点，以AP为直角作等腰直角三角形APD，∠APD=90°（点D落在第四象限）

(1)、当点P的坐标为（﹣1，0）时，求点D的坐标；

(2)、点P在移动的过程中，点D是否在直线y=x﹣2上？请说明理由；

(3)、连接OB交AD于点G，求证：AG=DG．

查看试题解析

植树品种	甲种	乙种	丙种	丁种
植树棵数	150		125	125