安徽省黄山市2018-2019学年高二上学期文数期中考试试卷

试卷更新日期：2019-10-10 类型：期中考试

进入出卷网下载

一、单选题

1. 和直线l都垂直的直线a，b的位置关系是（）

A、平行 B、平行或相交 C、平行或异面 D、平行、相交或异面

查看试题解析
2. 直线 $x + y - 3 = 0$ 的倾斜角是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{3 π}{4}$

查看试题解析
3. 如图，空间四边形ABCD中，E，F分别是AB，AD的中点，则EF与平面BCD的位置关系是（）

A、相交 B、平行 C、在平面内 D、不能确定

查看试题解析
4. 给出下列命题：
$①$ 存在每个面都是直角三角形的四面体； $②$ 若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直； $③$ 棱台的侧棱延长后交于一点； $④$ 用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台；其中正确命题的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 将半径为6的半圆围成一个圆锥的侧面，则此圆锥的体积为（）

A、 $3 \sqrt{3} π$ B、 $9 \sqrt{3} π$ C、 $12 \sqrt{3} π$ D、 $27 \sqrt{3} π$

查看试题解析
6. 一个空间几何体的三视图如图所示，则该几何体的体积是（）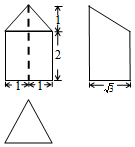

A、 $\frac{5}{3} \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\frac{7}{3} \sqrt{3}$ D、 $\frac{8}{3} \sqrt{3}$

查看试题解析
7. 四棱锥 $P - A B C D$ 的八条棱所在的直线中，任取两条能构成异面直线的共有（）对．

A、6 B、8 C、12 D、16

查看试题解析
8. 已知三棱锥 $S - A B C$ 的所有顶点都在球 $O$ 的球面上， $S A ⊥$ 平面 $A B C ， S A = 2 \sqrt{3} ， A B = 1 ， A C = 2 ， ∠ B A C = 60^{\circ}$ ，则球 $O$ 的体积为（）

A、 $4 π$ B、 $\frac{32}{3} π$ C、 $\frac{16}{3} π$ D、 $12 π$

查看试题解析
9. 在四棱锥 $P - A B C D$ 中，底面ABCD是边长为3的正方形， $P A ⊥$ 平面ABCD，且 $P A = \sqrt{6}$ ，则PC与平面ABCD所成角的大小为（）

A、 $30^{\circ}$ B、 $45^{\circ}$ C、 $60^{\circ}$ D、 $75^{\circ}$

查看试题解析
10. 设 $A (2 ， 3)$ ， $B (- 1 ， 2)$ ，若直线 $x + a y - 1 = 0$ 与线段AB相交，则a的取值范围是（）

A、 $[- 1 ， 3]$ B、 $[- 3 ， 1]$ C、 $[- \frac{1}{3} ， 1]$ D、 $(- \infty ， - \frac{1}{3}] \cup^{} [1 ， + \infty)$

查看试题解析
11. 对于直线m、n和平面 $α$ ，下面命题中的真命题是（）

A、如果 $m \subset α$ ， $n ⊄ α$ ，m、n是异面直线，那么 $n / / α$ B、如果 $m \subset α$ ， $n ⊄ α$ ，m、n是异面直线，那么n与 $α$ 相交 C、如果 $m \subset α$ ， $n / / α$ ，m、n共面，那么 $m / / n$ D、如果 $m / / α$ ， $n / / α$ ，m、n共面，那么 $m / / n$

查看试题解析
12. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，线段 $B_{1} D_{1}$ 上有两个动点E，F，且 $E F = \frac{1}{2}$ ，则 $① A C ⊥ B E$ ； $② E F / /$ 平面ABCD； $③$ 三棱锥 $B - A E F$ 的体积是定值； $④ △ A E F$ 的面积和 $△ B E F$ 的面积相等．以上命题中正确的是（）

A、 $① ②$ B、 $① ② ④$ C、 $① ② ③$ D、 $① ③ ④$

查看试题解析

二、填空题

13. 过平面外两点，可作个平面与已知平面平行．

查看试题解析
14. 设 $A (4 ， 2)$ ， $B (2 ， a)$ ，直线AB的斜率为3，则 $a =$ ．

查看试题解析
15. 在三棱锥 $A - B C D$ 中，E，F，G分别是AB，AC，BD的中点，若AD与BC所成的角是 $60^{\circ}$ ，那么 $∠ F E G$ 为．

查看试题解析
16. 在三棱锥 $A - B C D$ 中， $A B = C D = 8$ ， $A C = B D = 7$ ， $A D = B C = 5$ ，则该三棱锥的外接球的表面积为．

查看试题解析

三、解答题

17. 已知 $△ A B C$ 的点 $A (1 ， 3)$ ， $B (2 ， 7)$ ， $C (- 3 ， 4)$ ．

(1)、判断 $△ A B C$ 的形状；

(2)、设D，E分别为AB，AC的中点，求直线DE的斜率；

查看试题解析
18. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，设E为 $D D_{1}$ 的中点．

(1)、求异面直线BE与 $A D_{1}$ 所成的角；

(2)、设正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为a，求四面体 $A C B_{1} D_{1}$ 的体积．

查看试题解析
19. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧棱垂直于底面， $A B ⊥ B C$ ，E、F分别为 $A_{1} C_{1}$ 、BC的中点．

(1)、求证： $C_{1} F / /$ 平面ABE；

(2)、求证：平面 $A B E ⊥$ 平面 $B_{1} B C C_{1}$ ．

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中， $A P ⊥$ 面ABCD， $A D / / B C$ ， $A B = B C = \frac{1}{2} A D$ ，E，F分别为线段AD，PA的中点．

(1)、求证：平面 $P C D / /$ 平面BEF；

(2)、求证： $B E ⊥$ 平面PAC．

查看试题解析
21. 如图，正三棱锥 $P - A B C$ 的底边长为3，其侧棱长为 $\sqrt{7}$ ，设D为PC的中点．

(1)、求证： $P A ⊥ B C$ ；

(2)、求BD与底面ABC所成角的正弦值．

查看试题解析
22. 如图，在四棱锥 $P - A B C D$ 中，底面是以O为中心的菱形， $P O ⊥$ 底面ABCD， $A B = 2$ ， $∠ B A D = \frac{π}{3}$ ，M为BC上一点．

(1)、当BM等于多少时， $B C ⊥$ 平面POM？

(2)、在满足 $(1)$ 的条件下，若 $M P ⊥ A P$ ，求四棱锥 $P - A B M O$ 的体积．

查看试题解析