安徽省安庆市五校联盟2018-2019学年高二上学期理数期中考试试卷

试卷更新日期：2019-10-10 类型：期中考试

进入出卷网下载

一、单选题

1. 直线 $\sqrt{3} x - y - 2018 = 0$ 的倾斜角等于（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{4}$ D、不存在

查看试题解析
2. 平行于直线x+2y+1=0且与圆x²+y²=4相切的直线的方程是（）

A、x+2y+5=0或x+2y﹣5=0 B、 $x + 2 y + 2 \sqrt{5} = 0$ 或 $x + 2 y - 2 \sqrt{5} = 0$ C、2x﹣y+5=0或2x﹣y﹣5=0 D、 $x - 2 y + \sqrt{5} = 0$ 或 $x - 2 y - \sqrt{5} = 0$

查看试题解析
3. 某工厂利用随机数表对生产的700个零件进行抽样测试，先将700个零件进行编号，001,002,……，699,700.从中抽取70个样本，下图提供随机数表的第4行到第6行，若从表中第5行第6列开始向右读取数据，则得到的第6个样本编号是（）
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42

84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04

32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45

A、623 B、328 C、253 D、007

查看试题解析
4. 某单位为了了解用电量y（度）与气温x（℃）之间的关系，记录了某4天的用电量与当天气温，数据如表所示：

气温x（℃）

17

13

8

2

用电量y（度）

24

33

40

55

用最小二乘法求得回归直线方程为 $\hat{y} = \hat{b} x + 58$ ，则 $\hat{b}$ 的值为（）

A、﹣2.25 B、﹣2 C、﹣1.6 D、﹣1.5

查看试题解析
5. 执行下面的程序框图，则输出 $K$ 的值为（）

A、98 B、99 C、100 D、101

查看试题解析
6. 已知圆C₁：（x+a）²+（y﹣2）²=1与圆C₂：（x﹣b）²+（y﹣2）²=4相外切，a ， b为正实数，则ab的最大值为（）

A、 $2 \sqrt{3}$ B、 $\frac{9}{4}$ C、 $\frac{3}{2}$ D、 $\frac{\sqrt{6}}{2}$

查看试题解析
7. 已知点Q是点P（5，4，3）在平面xOy上的射影，则线段PQ的长等于（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如果数据x₁ ， x₂ ， …x_n的平均数为 $\bar{x}$ ，方差为s² ，则5x₁+2，5x₂+2，…，5x_n+2的平均数和方差分别为（）

A、 $\bar{x}$ ，s² B、5 $\bar{x}$ +2，s² C、5 $\bar{x}$ +2，25s² D、 $\bar{x}$ ，25s²

查看试题解析
9. 在学校组织的考试中，45名学生的数学成绩的茎叶图如图所示，则该45名学生的数学成绩的中位数为（）

A、127 B、128 C、128.5 D、129

查看试题解析
10. 已知圆C：（x﹣1）²+（y﹣4）²=10和点M（5，t），若圆C上存在两点A，B，使得MA⊥MB，则实数t的取值范围为（）

A、[﹣2，6] B、[﹣3，5] C、[2，6] D、[3，5]

查看试题解析
11. 袋中装有3个黑球，4个白球，从中任取4个球，则
①至少有1个白球和至少有1个黑球；②至少有2个白球和恰有3个黑球；③至少有1个黑球和全是白球；④恰有1个白球和至多有1个黑球．在上述事件中，是互斥事件但不是对立事件的为（）

A、① B、② C、③ D、④

查看试题解析
12. 若直线 $y = x + b$ 与曲线 $y = 3 - \sqrt{4 x - x^{2}}$ 有公共点，则 $b$ 的取值范围是（）

A、 $[1 - \sqrt{2} ， 1 + \sqrt{2}]$ B、 $[1 - \sqrt{2} ， 3]$ C、 $[1 - 2 \sqrt{2} ， 3]$ D、 $[- 1 ， 1 + \sqrt{2}]$

查看试题解析

二、填空题

13. 直线 $(a - 1) x - y + 2 a + 1 = 0$ 恒过定点．

查看试题解析
14. 某高中校高一、高二、高三三个年级人数分别为300，300，400通过分层抽样从中抽取40人进行问卷调查，高三抽取的人数是．

查看试题解析
15. 一名射箭运动员5次射箭命中环数的“茎叶图”如图，则他5次射箭命中环数的方差为．

查看试题解析
16. 直线 $l : 3 x - 4 y + 2 = 0$ 与圆 $x^{2} + y^{2} + 2 x - 2 y - 2 = 0$ 相交于A ， B两点，则线段AB的长为．

查看试题解析

三、解答题

17. 已知圆C的圆心在直线x﹣2y﹣3=0上，并且经过A（2，﹣3）和B（﹣2，﹣5），求圆C的标准方程．

查看试题解析
18. 去年“十•一”期间，昆曲高速公路车辆较多．某调查公司在曲靖收费站从7座以下小型汽车中按进收费站的先后顺序，每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查，将他们在某段高速公路的车速（ $k m / h$ ）分成六段： $[60 ， 65)$ ， $[65 ， 70)$ ， $[70 ， 75)$ ， $[75 ， 80)$ ， $[80 ， 85)$ ， $[85 ， 90)$ 后，得到如图的频率分布直方图．

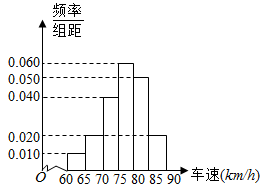
（I）调查公司在抽样时用到的是哪种抽样方法？

（II）求这40辆小型汽车车速的众数和中位数的估计值；

（III）若从这40辆车速在 $[60 ， 70)$ 的小型汽车中任意抽取2辆，求抽出的2辆车车速都在 $[65 ， 70)$ 的概率．

查看试题解析
19. 有一个同学家开了一个奶茶店，他为了研究气温对热奶茶销售杯数的影响，从一季度中随机选取5天，统计出气温与热奶茶销售杯数，如表：

气温 $x (° C)$

0

4

12

19

27

热奶茶销售杯数 $y$

150

132

130

104

94

（Ⅰ）求热奶茶销售杯数关于气温的线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ （ $\hat{b}$ 精确到0.1），若某天的气温为 $15 ° C$ ，预测这天热奶茶的销售杯数；

（Ⅱ）从表中的5天中任取两天，求所选取两天中至少有一天热奶茶销售杯数大于130的概率．

参考数据： $4^{2} + 12^{2} + 19^{2} + 27^{2} = 1250$ ， $4 \times 132 + 12 \times 130 + 19 \times 104 + 27 \times 94 = 6602$ .

参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

查看试题解析
20. 如图，已知矩形 $A B C D$ 四点坐标为A（0，-2），C（4，2），B（4，-2），D（0，2）．

(1)、求对角线 $A C$ 所在直线的方程；

(2)、求矩形 $A B C D$ 外接圆的方程；

(3)、若动点 $P$ 为外接圆上一点，点 $N (- 2 ， 0)$ 为定点，问线段PN中点的轨迹是什么，并求出该轨迹方程。

查看试题解析
21. 甲乙两人各有相同的小球10个，在每人的10个小球中都有5个标有数字1，3个标有数字2，2个标有数字3。两人同时分别从自己的小球中任意抽取1个，规定：若抽取的两个小球上的数字相同，则甲获胜，否则乙获胜，求乙获胜的概率。

查看试题解析
22. 已知圆C：（x﹣2）²+（y﹣3）²=16及直线l：（m+2）x+（3m+1）y=15m+10（m∈R）．

(1)、证明：不论m取什么实数，直线l与圆C恒相交；

(2)、求直线l被圆C截得的弦长的最短长度及此时的直线方程．

查看试题解析

气温 $x (° C)$	0	4	12	19	27
热奶茶销售杯数 $y$	150	132	130	104	94

气温x（℃）	17	13	8	2
用电量y（度）	24	33	40	55