2017年江苏省无锡市中考数学试卷
试卷更新日期:2017-06-28 类型:中考真卷
一、选择题
-
1. ﹣5的倒数是( )A、 B、±5 C、5 D、﹣2. 函数y= 中自变量x的取值范围是( )A、x≠2 B、x≥2 C、x≤2 D、x>23. 下列运算正确的是( )A、(a2)3=a5 B、(ab)2=ab2 C、a6÷a3=a2 D、a2•a3=a54. 下列图形中,是中心对称图形的是( )A、
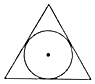 B、
B、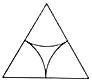 C、
C、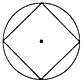 D、
D、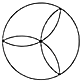 5. 若a﹣b=2,b﹣c=﹣3,则a﹣c等于( )A、1 B、﹣1 C、5 D、﹣56. “表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
5. 若a﹣b=2,b﹣c=﹣3,则a﹣c等于( )A、1 B、﹣1 C、5 D、﹣56. “表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )成绩(分)
70
80
90
男生(人)
5
10
7
女生(人)
4
13
4
A、男生的平均成绩大于女生的平均成绩 B、男生的平均成绩小于女生的平均成绩 C、男生成绩的中位数大于女生成绩的中位数 D、男生成绩的中位数小于女生成绩的中位数7. 某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、25% C、50% D、62.5%8. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=﹣3,b=2 C、a=3,b=﹣1 D、a=﹣1,b=39. 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )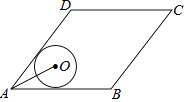 A、5 B、6 C、2 D、310. 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
A、5 B、6 C、2 D、310. 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )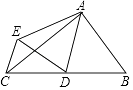 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 计算 × 的值是 .12. 分解因式:3a2﹣6a+3= .13. 贵州FAST望远镜是目前世界第一大单口径射电望远镜,反射面总面积约250000m2 , 这个数据用科学记数法可表示为 .14. 如图是我市某连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是℃.
 15. 若反比例函数y= 的图象经过点(﹣1,﹣2),则k的值为 .16. 若圆锥的底面半径为3cm,母线长是5cm,则它的侧面展开图的面积为 cm2 .17. 如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2 , 一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由 ,EF, ,AB所围成图形(图中阴影部分)的面积等于 .
15. 若反比例函数y= 的图象经过点(﹣1,﹣2),则k的值为 .16. 若圆锥的底面半径为3cm,母线长是5cm,则它的侧面展开图的面积为 cm2 .17. 如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2 , 一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由 ,EF, ,AB所围成图形(图中阴影部分)的面积等于 . 18. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .
18. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .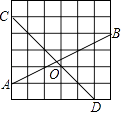
三、解答题
-
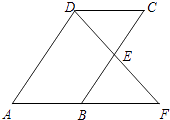
19. 计算:(1)、|﹣6|+(﹣2)3+( )0;(2)、(a+b)(a﹣b)﹣a(a﹣b)20.(1)、解不等式组:(2)、解方程: = .21. 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
 22. 甲、乙、丙、丁四人玩扑克牌游戏,他们先取出两张红心和两张黑桃共四张扑克牌,洗匀后背面朝上放在桌面上,每人抽取其中一张,拿到相同颜色的即为游戏搭档,现甲、乙两人各抽取了一张,求两人恰好成为游戏搭档的概率.(请用“画树状图”或“列表”等方法写出分析过程)23. 某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
22. 甲、乙、丙、丁四人玩扑克牌游戏,他们先取出两张红心和两张黑桃共四张扑克牌,洗匀后背面朝上放在桌面上,每人抽取其中一张,拿到相同颜色的即为游戏搭档,现甲、乙两人各抽取了一张,求两人恰好成为游戏搭档的概率.(请用“画树状图”或“列表”等方法写出分析过程)23. 某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:时间
第1天
第2天
第3天
第4天
第5天
新加入人数(人)
153
550
653
b
725
累计总人数(人)
3353
3903
a
5156
5881
 (1)、表格中a= , b=;(2)、请把下面的条形统计图补充完整;(3)、根据以上信息,下列说法正确的是(只要填写正确说法前的序号).
(1)、表格中a= , b=;(2)、请把下面的条形统计图补充完整;(3)、根据以上信息,下列说法正确的是(只要填写正确说法前的序号).①在活动之前,该网站已有3200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2528人.
24. 如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):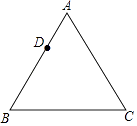 (1)、作△ABC的外心O;(2)、设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.25.
(1)、作△ABC的外心O;(2)、设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.25.操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
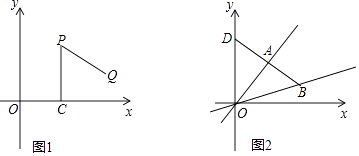 (1)、点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,﹣ ),则点M的坐标为 .(2)、A是函数y= x图象上异于原点O的任意一点,经过T变换后得到点B.
(1)、点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,﹣ ),则点M的坐标为 .(2)、A是函数y= x图象上异于原点O的任意一点,经过T变换后得到点B.①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
26. 某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:污水处理器型号
A型
B型
处理污水能力(吨/月)
240
180
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)、求每台A型、B型污水处理器的价格;(2)、为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?27. 如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2. (1)、求点P的坐标;(2)、求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.28.
(1)、求点P的坐标;(2)、求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.28.如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
 (1)、若m=6,求当P,E,B三点在同一直线上时对应的t的值.(2)、已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
(1)、若m=6,求当P,E,B三点在同一直线上时对应的t的值.(2)、已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.