云南省易门县2019届九年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，属于一元二次方程的是（）

A、ax²+bx+c=0 B、 $x^{2} - \frac{2}{x} = 3$ C、（x+3）²=2（x﹣3） D、（x+4）（x﹣2）=x²

查看试题解析
3. 已知函数 $y = (m + 2) x^{m^{2} - 2}$ 是二次函数，则 $m$ 等于（）

A、±2 B、2 C、-2 D、±1

查看试题解析
4. 如图，将 $Rt △ A B C$ 绕直角顶点 $C$ 顺时针旋转 $90 °$ ，得到 $△ A^{'} B^{'} C^{'}$ ，连接 $A A^{'}$ ，若 $∠ 1 = 25 °$ ，则 $∠ B A A^{'}$ 的度数是（）

A、 $55 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
5. 一元二次方程x²﹣6x﹣5=0配方可变形为（）

A、（x﹣3）²=14 B、（x﹣3）²=4 C、（x+3）²=14 D、（x+3）²=4

查看试题解析
6. 当ab＞0时，y＝ax²与y＝ax＋b的图象大致是（）

A、 B、 C、 D、

查看试题解析
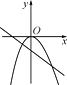7. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则下
列结论：① $a b c < 0$ ，② $b < a + c$ ，③ $4 a + 2 b + c > 0$ ，④ $2 c < 3 b$ ，⑤ $a + b < m (a m + b)$ $(m \neq 1)$ 中正确的是（）

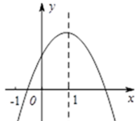A、②④⑤ B、①②④ C、①③④ D、①③④⑤

查看试题解析

二、填空题

8. 已知点M的坐标为（－2，－3），则点M关于原点对称的坐标为．

查看试题解析
9. 一元二次方程（x+1）(3x－2)=8的一般形式是 .

查看试题解析
10. 已知抛物线的顶点为（1，﹣3），且过点（2，1），求这个函数的表达式为.

查看试题解析
11. 关于 $x$ 的一元二次方程 $x^{2} + 2 x - 2 m + 1 = 0$ 的两实数根之积为负，则实数 $m$ 的取值范围是.

查看试题解析
12. 设 A（﹣2，y₁），B（1，y₂），C（2，y₃）是抛物线 y=（x﹣1）²﹣3上的三点，则 y₁ ， y₂ ， y₃ 的大小关系为.

查看试题解析
13.
如图，两块相同的三角板完全重合在一起，∠A=30°，AC=10，把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置，点C′在AC上，A′C′与AB相交于点D，则C′D=

查看试题解析

三、解答题

14. 解方程：

(1)、2x²﹣5x﹣3=0

(2)、（x﹣3）²+2x（x﹣3）=0.

查看试题解析
15. 组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，则比赛组织者应邀请多少个队参赛？

查看试题解析
16. 如图，在△ABC中，∠C＝90°，AC＝2cm，AB＝3cm，将△ABC绕点B顺时针旋转60°得到△FBE，求点E与点C之间的距离.

查看试题解析
17. 把二次函数y=a(x-h)²+k的图象先向左平移2个单位，再向上平移4个单位，得到二次函数y= $\frac{1}{2}$ (x+1)²-1的图象.

(1)、试确定a，h，k的值；

(2)、指出二次函数y=a(x-h)²+k的开口方向，对称轴和顶点坐标.

查看试题解析
18. 已知关于x的方程x²－(k＋2)x＋2k＝0．

(1)、求证：k取任何实数值，方程总有实数根；

(2)、若Rt△ABC斜边长a＝3，另两边长b，c恰好是这个方程的两个根，求△ABC的周长．

查看试题解析
19. 在某市组织的大型商业演出活动中，对团体购买门票实行优惠，决定在原定票价基础上每张降价80元，这样按原定票价需花费6000元购买的门票张数，现在只花费了4800元.

(1)、求每张门票原定的票价；

(2)、根据实际情况，活动组织单位决定对于个人购票也采取优惠措施，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率.

查看试题解析
20. 某商场销售一批名牌衬衫，平均每天可售出 20 件，每件盈利 45 元，为了扩大销售、增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价 1 元.商场平均每天可多售出 4 件，

(1)、若商场平均每天盈利最大，每件衬衫应降价多少元？

(2)、每天可售出多少件？

查看试题解析
21. 如图，在边长为1的小正方形网格中，△AOB的顶点均在格点上，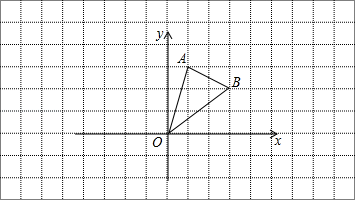

(1)、B点关于y轴的对称点坐标为；

(2)、①将△AOB向左平移3个单位长度得到△A₁O₁B₁ ，请画出△A₁O₁B₁；
②以原点O为对称中心，画出△ AOB与关于原点成中心对称的△ A₂ O B₂；

③以原点O为旋转中心，画出把△AOB顺时针旋转90°的图形△A₃ O B₃.

查看试题解析
22. 如图，抛物线y＝ax²+3x+c经过A（﹣1，0），B（4，0）两点，与y轴交于点C.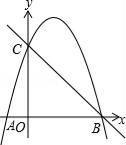

(1)、求抛物线的解析式；

(2)、若点P在第一象限的抛物线上，且点P的横坐标为t，过点P向x轴作垂线交直线BC于点Q，设线段PQ的长为m，求m与t之间的函数关系式，并求出m的最大值；

(3)、在x轴上是否存在点E，使以点B，C，E为顶点的三角形为等腰三角形？如果存在，直接写出E点坐标；如果不存在，请说明理由.

查看试题解析