湖北省宜昌市2019届九年级上学期期中考试数学试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列汽车标志中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程 $3 x^{2} - 4 x - 1 = 0$ 的二次项系数和一次项系数分别为（）

A、3，-1 B、3，-4 C、3，4 D、 $3 x^{2}$ ， $- 4 x$

查看试题解析
3. 方程x²=2x的解是（）

A、x=0 B、x=2 C、x₁=0，x₂=2 D、x₁=0，x₂= $\sqrt{2}$

查看试题解析
4. 若 $m$ 、 $n$ 是一元二次方程 $x^{2} - 5 x + 2 = 0$ 的两个实数根，则 $m + n - m n$ 的值是（）

A、7 B、-7 C、3 D、-3

查看试题解析
5. 若 $a$ 为方程 $x^{2} + x - 5 = 0$ 的解，则 $a^{2} + a + 1$ 的值为（）

A、 $12$ B、16 C、9 D、6

查看试题解析
6. 将抛物线y=2x²向左平移1个单位,再向上平移3个单位得到的抛物线,其解析式是( )

A、y=2(x+1)²+3 B、y=2(x－1)²－3 C、y=2(x+1)²－3 D、y=2(x－1)²+3

查看试题解析
7. 抛物线 $y = \frac{1}{2} {(x + 2)}^{2} + 1$ 的顶点坐标是（）

A、(2， 1) B、(-2， 1) C、(2， -1) D、(-2， -1)

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c$ 的 $x$ 、 $y$ 的部分对应值如下表：
$x$
$- 1$
$0$
$1$
$2$
$3$
$y$
$5$
$1$
$- 1$
$- 1$
$1$
则该二次函数图象的对称轴为（）

A、y轴 B、直线 $x = \frac{5}{2}$ C、直线x=2 D、直线 $x = \frac{3}{2}$

查看试题解析
9. 关于x的一元二次方程9x²-6x+k=0有两个不相等的实根，则k的范围是（）

A、 $k < 1$ B、 $k > 1$ C、 $k \leq 1$ D、 $k \geq 1$

查看试题解析
10. 如图，矩形 $O A B C$ 的顶点 $O$ 为坐标原点，点 $A$ 在 $x$ 轴上，点 $B$ 的坐标为 $(2 ， 1)$ .如果将矩形 $O A B C$ 绕点 $O$ 旋转 $180^{\circ}$ 旋转后的图形为矩形 $O A_{1} B_{1} C_{1}$ ，那么点 $B_{1}$ 的坐标为（）

A、(2， 1) B、(-2， 1) C、(-2， -1) D、(2， -l)

查看试题解析
11. 如图， $△ A B C$ 中，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $40^{\circ}$ 后，得到 $△ A B' C'$ ，且 $C'$ 在边 $B C$ 上，则 $∠ A C' C$ 的度数为（）

A、 $50^{\circ}$ B、 $60^{\circ}$ C、 $70^{\circ}$ D、 $80^{\circ}$

查看试题解析
12. 已知⊙O的半径为4cm，A为线段OP的中点，当OP=7cm时，点A与⊙O的位置关系是（）

A、点A在⊙O内 B、点A在⊙O上 C、点A在⊙O外 D、不能确定

查看试题解析
13. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，连结 $O A$ 、 $O B$ ，且点 $C$ 、 $O$ 在弦 $A B$ 的同侧，若 $∠ A B O = 50^{\circ}$ ，则 $∠ A C B$ 的度数为（）

A、 $50^{\circ}$ B、 $45^{\circ}$ C、 $40^{\circ}$ D、 $30^{\circ}$

查看试题解析
14. ⊙O的直径为10，圆心O到弦AB的距离为3，则弦AB的长是（）

A、4 B、6 C、7 D、8

查看试题解析
15. 已知二次函数y=ax²+bx+c的图象如图，其对称轴x=﹣1，给出下列结果：
①b²＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a﹣b+c＜0，
则正确的结论是（）

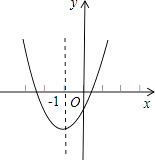A、①②③④ B、②④⑤ C、②③④ D、①④⑤

查看试题解析

二、解答题

16. 解方程： $x^{2} - 6 x = 1$

查看试题解析
17. 已知关于 $x$ 的方程 $x^{2} - 2 (k - 1) x + k^{2} = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ．

(1)、求 $k$ 的取值范围；

(2)、若 $| x_{1} + x_{2} | = x_{1} x_{2} - 1$ ，求 $k$ 的值．

查看试题解析
18. 如图，点 $O$ 是等边 $△ A B C$ 内一点， $∠ A O B = 110^{\circ}$ ， $∠ B O C = α$ ，将 $△ B O C$ 绕点 $C$ 按顺时针方向旋转 $60^{\circ}$ 得 $△ A D C$ ，连接 $O D$ .

(1)、求证： $△ C O D$ 是等边三角形；

(2)、当 $α = 150^{\circ}$ 时，试判断 $△ A O D$ 的形状，并说明理由.

查看试题解析
19. 如图，在⊙O中，AB是直径，CD是弦，AB⊥CD.

(1)、P是 $\overset{⌢}{C A D}$ 上一点（不与C、D重合），求证：∠CPD=∠COB；

(2)、点P′在劣弧CD上（不与C、D重合）时，∠CP′D与∠COB有什么数量关系？请证明你的结论.

查看试题解析
20. 如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．

(1)、将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△ $A_{1} B_{1}$ C；平移△ABC，若A的对应点 $A_{2}$ 的坐标为（0，4），画出平移后对应的△ $A_{2} B_{2} C_{2}$ ；

(2)、若将△ $A_{1} B_{1}$ C绕某一点旋转可以得到△ $A_{2} B_{2} C_{2}$ ，请直接写出旋转中心的坐标；

(3)、在轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．

查看试题解析
21. 某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系)．
根据图象提供的信息，解答下列问题：

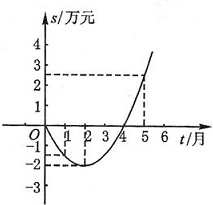(1)、由已知图象上的三点坐标，求累积利润s(万元)与时间t(月)之间的函数关系式；

(2)、求截止到几月末公司累积利润可达到30万元；

(3)、求第8个月公司所获利润为多少万元?

查看试题解析
22. 长城科技公司生产销售一种电子产品，该产品总成本包括技术成本、制造成本、销售成本三部分，经核算，2014年该产品各部分成本所占比例约为2：a：1．且2014年该产品的技术成本、制造成本分别为400万元、1400万元．

(1)、确定a的值，并求2014年产品总成本为多少万元；

(2)、为降低总成本，该公司2015年及2016年增加了技术成本投入，确保这两年技术成本都比前一年增加一个相同的百分数m（m＜50%），制造成本在这两年里都比前一年减少一个相同的百分数2m；同时为了扩大销售量，2016年的销售成本将在2014年的基础上提高10%，经过以上变革，预计2016年该产品总成本达到2014年该产品总成本的 $\frac{4}{5}$ ，求m的值．

查看试题解析
23. 正方形 $A B C D$ 中，将一个直角三角板的直角顶点与点 $A$ 重合，一条直角边与边 $B C$ 交于点 $E$ （点 $E$ 不与点 $B$ 和点 $C$ 重合），另一条直角边与边 $C D$ 的延长线交于点 $F$ .

(1)、如图①，求证： $A E = A F$ ；

(2)、如图②，此直角三角板有一个角是 $45^{\circ}$ ，它的斜边 $M N$ 与边 $C D$ 交于 $G$ ，且点 $G$ 是斜边 $M N$ 的中点，连接 $E G$ ，求证： $E G = B E + D G$ ；

(3)、在 $(2)$ 的条件下，如果 $\frac{A B}{G F} = \frac{6}{5}$ ，那么点 $G$ 是否一定是边 $C D$ 的中点？请说明你的理由.

查看试题解析
24. 如图 $1$ ，若抛物线 $L_{1}$ 的顶点 $A$ 在抛物线 $L_{2}$ 上，抛物线 $L_{2}$ 的顶点 $B$ 也在抛物线 $L_{1}$ 上（点 $A$ 与点 $B$ 不重合），我们定义：这样的两条抛物 $L_{1}$ ， $L_{2}$ 互为“友好”抛物线，可见一条抛物线的“友好”抛物线可以有多条.

(1)、如图 $2$ ，已知抛物线 $L_{3} ： y = 2 x^{2} - 8 x + 4$ 与 $y$ 轴交于点 $C$ ，试求出点 $C$ 关于该抛物线对称轴对称的点 $D$ 的坐标；

(2)、请求出以点 $D$ 为顶点的 $L_{3}$ 的友好抛物线 $L_{4}$ 的解析式，并指出 $L_{3}$ 与 $L_{4}$ 中 $y$ 同时随 $x$ 增大而增大的自变量的取值范围；

(3)、若抛物 $y = a_{1} {(x - m)}^{2} + n$ 的任意一条友好抛物线的解析式为 $y = a_{2} {(x - h)}^{2} + k$ ，请写出 $a_{1}$ 与 $a_{2}$ 的关系式，并说明理由.

查看试题解析

$x$	$- 1$	$0$	$1$	$2$	$3$
$y$	$5$	$1$	$- 1$	$- 1$	$1$