湖北省孝感市云梦县2019届九年级上学期数学期中考试试卷
试卷更新日期：2019-10-09 类型：期中考试
一、单选题
-
1. 小明在解方程x2﹣4x﹣7=0时，他是这样求解的：移项，得x2﹣4x=7，两边同时加4，得x2﹣4x+4=11，∴（x﹣2）2=11，∴x﹣2=± ，∴x1=2+ ，x2=2﹣ ，这种解方程的方法称为（ ）A、待定系数法 B、配方法 C、公式法 D、因式分解法2. 下列四个图形中，不是中心对称图形的是（ ）A、
B、
C、
D、
3. 将二次函数 y=x2的图象先向右平移 1 个单位长度，再向下平移 2 个单位长度，可以得到函数（ ）的图象．A、y=（x﹣1）2+2 B、y=（x﹣1）2﹣2 C、y=（x+1）2+2 D、y=（x+1）2﹣24. 关于x的一元二次方程（a﹣1）x2+x+a2﹣1=0的一个根是0，则a的值为（ ）A、﹣1 B、1 C、1或﹣1 D、0.55. 某药品经过两次降价，每瓶零售价由 156 元降为 118 元．已知两次降价的百分率相同每次降价的百分率为 x，根据题意列方程得（ ）A、156（1+x）2=118 B、156（1﹣x2）=118 C、156（1﹣2x）=118 D、156（1﹣x）2=1186. 已知关于 x 的一元二次方程 x2+mx﹣3=0 一个根为 3，则另一个根为（ ）A、1 B、﹣1 C、2 D、﹣67. 如图，在△ABC 中，∠C=90°，∠BAC=70°，将△ABC 绕点 A 顺时针旋转 70°，B，C 旋转后的对应点分别是 B′和 C′，连接 BB′，则∠B′BC′的度数是（ ）
A、35° B、40° C、50° D、55°8. 在平面直角坐标系中，二次函数 y1=﹣x2+4x 和一次函数 y2=2x 的图象如图所示，那么不等式﹣x2+4x＞2x 的解集是（ ）
A、x＜0 B、0＜x＜4 C、0＜x＜2 D、2＜x＜49. 如图，B，C是⊙A上的两点，AB的垂直平分线与⊙A交于E，F两点，与线段AC交于点D．若∠BFC=18°，则∠DBC=（ ）
A、30° B、32° C、36° D、40°二、填空题
-
10. 已知点A（a，1）与点A（4，b）关于原点对称，则a+b＝ ．11. 若方程 x2﹣5x﹣1=0 的两根为 x1 ， x2 ， 则 x1·x2﹣x1﹣x2= ．12. 抛物线y=x2﹣3x﹣15 与x 轴的一个交点是（m，0），则2m2﹣6m 的值为 ．13. 在圆内接四边形ABCD中，∠A、∠B、∠C的度数之比为3：4：6，则∠D=度．14. 把二次函数y=（x﹣2）2+1的图象绕原点旋转180°后得到的图象的解析式为 ．15. 如图，在直角坐标系中，已知点 A（﹣3，0），B（0，4），对△OAB 连续作旋转变换，依次得到三角形（1），（2），（3），（4）…，则三角形（2019）的直角顶点的坐标为 ．
三、解答题
-
16. 用指定的方法解下列方程：(1)、2x2﹣3x+1=0（配方法）(2)、4x2﹣4 x﹣1=0（公式法）17. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：
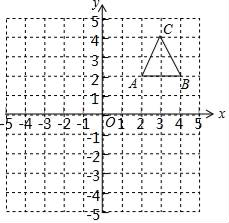
①画出△ABC关于y轴对称的△A1B1C1 ， 并写出A1的坐标．
②画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2 ， 并写出A2的坐标．
③画出△A2B2C2关于原点O成中心对称的△A3B3C3 ， 并写出A3的坐标．
18. 如图所示的是水面一桥拱的示意图，它的形状类似于抛物线，在正常水位时，该桥下水面宽度为20米，拱顶距离正常水面4米，建立平面直角坐标系如图所示，求抛物线的解析式．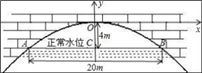
19. 已知关于x的一元二次方程（x﹣1）（x﹣2）＝m（m+1）(1)、试证明：无论m取何值此方程总有两个实数根；(2)、若原方程的两根x1 ， x2满足x12+x22﹣x1x2＝3m2+2，求m的值．20. 如图，已知⊙O 的直径 AB 垂直弦 CD 于点 E，连接 CO 并延长交 AD于点 F，且 CF⊥AD
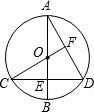(1)、求证：点 E 是 OB 的中点；(2)、若 AB=12，求 CD 的长．21. 某超市销售樱桃，已知樱桃的进价为14元/千克，如果售价为20元/千克，那么每天可售出 260 千克，如果售价为25元/千克，那么每天可售出210千克，经调查发现：每天的销售量y（千克）与售价 x（元/千克）之间存在一次函数关系(1)、求y与x之间的函数关系式；(2)、若该超市每天要获得利润 1920 元，同时又要让消费者得到实惠，则售价 x应定于多少元？(3)、若樱桃的售价不得高于 28 元/千克，请问售价定为多少时，该超市每天销售樱桃所获的利润最大？最大利润是多少元？22. 如图
(1)、问题发现：如图①，△ABC 和△AED 都是等腰直角三角形，∠BAC=∠EAD=90°，点 B 在线段AE 上，点 C 在线段AD 上，请直接写出线段 BE 与线段 CD 的数量与位置关系是关系：；
(2)、操作探究：如图②，将图①中的△ABC 绕点 A 顺时针旋转α（0°＜α＜360°），（1）小题中线段 BE 与线段 CD 的关系是否成立？如果不成立，说明理由，如果成立，请你结合图②给出的情形进行证明；
(3)、解决问题：将图①中的△ABC 绕点 A 顺时针旋转α（0°＜α＜360°），若 DE=2AC，在旋转的过程中，当以 A、B、C、D 四点为顶点的四边形是平行四边形时，在备用图中画出其中的一个情形，并写出此时旋转角α的度数是度．
23. 如图，抛物线y=﹣ x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．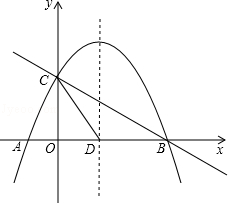
(1)、求抛物线的表达式；(2)、在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；(3)、点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．