湖北省武汉市硚口区2019届九年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 若关于x的方程ax²﹣3x﹣2＝0是一元二次方程，则（）

A、a＞1 B、a≠0 C、a＝1 D、a≥0

查看试题解析
2. 下列图形中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 用配方法解一元二次方程x²﹣6x+8=0时，则方程变形正确的是（）

A、（x﹣3）²=17 B、（x+3）²=17 C、（x﹣3）²=1 D、（x+3）²=1

查看试题解析
4. 抛物线y=﹣ $\frac{1}{2}$ x²向左平移1个单位长度得到抛物线的解析式为（）

A、y=﹣ $\frac{1}{2}$ （x+1）² B、y=﹣ $\frac{1}{2}$ （x﹣1）² C、y=﹣ $\frac{1}{2}$ x²+1 D、y=﹣ $\frac{1}{2}$ x²﹣1

查看试题解析
5. 对于抛物线y＝﹣2（x﹣1）²+3，下列判断正确的是（）

A、抛物线的开口向上 B、抛物线的顶点坐标是（﹣1，3） C、对称轴为直线x＝1 D、当x＝3时，y＞0

查看试题解析
6. 如图，AB，AC，BC都是⊙O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N，若MN＝1，则BC的值为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 设A（﹣2，y₁），B（1，y₂），C（2，y₃）是抛物线y=﹣（x+1）²+3上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A、y₁＞y₂＞y₃ B、y₁＞y₃＞y₂ C、y₃＞y₂＞y₁ D、y₃＞y₁＞y₂

查看试题解析
8. 如图，将△ABC绕点A按逆时针方向旋转100°，得到△AB₁C₁ ，若点B₁在线段BC的延长线上，则∠BB₁C₁的大小为（）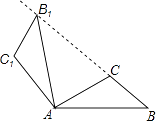

A、70° B、80° C、84° D、86°

查看试题解析
9. 函数y＝kx²﹣4x+2的图象与x轴有公共点，则k的取值范围是（）

A、k＜2 B、k＜2 且 k≠0 C、k≤2 D、k≤2 且 k≠0

查看试题解析
10. 如图，在平面直角坐标系中，已知A（0，2），M（m，0）且m＞0，分别以AO、AM为边在∠AOM内部作等边△AOB和等边△AMC，连接CB并延长交x轴于点D，则C点的横坐标的值为（）

A、 $\frac{1}{2}$ m+ $\frac{3 \sqrt{3}}{2}$ B、 $\frac{1}{2}$ m+ $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ m+ $\frac{2 \sqrt{3}}{3}$ D、 $\frac{1}{2}$ m+ $\sqrt{3}$

查看试题解析

二、填空题

11. 在平面直角坐标系中，点A（2，3）绕原点O逆时针旋转90°的对应点的坐标为．

查看试题解析
12. 某工厂七月份出口创汇200万美元，因受国际大环境的严重影响，出口创汇出现连续下滑，至九月份时出口创汇下降到只有98万美元，设该厂平均每月下降的百分率是x，则所列方程是.（可不必化成一般形式！）

查看试题解析
13. 某宾馆有40个房间供游客居住，当每个房间每天的定价为160元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲.如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用.设每间每天房价定为x元，宾馆每天利润为y元，则y与x的函数关系式为.

查看试题解析
14. 如图，将一个大平行四边形在一角剪去一个小平行四边形，如果用直尺画一条直线将其剩余部分分割成面积相等的两部分，这样的不同的直线一共可以画出条.

查看试题解析
15. 已知二次函数y＝x²﹣2x+2在t≤x≤t+1时的最小值是t，则t的值为.

查看试题解析

三、解答题

16. 如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，并且CD＝4，EM＝6，求⊙O的半径.

查看试题解析
17. 已知关于x的方程x²+(2k﹣1)x+k²﹣1＝0有两个实数根x₁ ， x₂.

(1)、求k的取值范围；

(2)、若x₁ ， x₂满足x₁x₂+x₁+x₂＝3，求k的值.

查看试题解析
18. 如图，△ABC的顶点坐标分别为A（﹣4，5），B（﹣5，2），C（﹣3，4）

(1)、画出与△ABC关于原点O对称的△A₁B₁C₁ ，并写出点A₁的坐标为；

(2)、D是x轴上一点，使DB+DC的值最小，画出点D（保留画图痕迹）；

(3)、P（t，0）是x轴上的动点，将点C绕点P顺时针旋转90°至点E，直线y＝﹣2x+5经过点E，则t的值为.

查看试题解析
19. 有一个抛物线型蔬菜大棚，将其截面放在如图所示的平面直角坐标系中，抛物线可以用函数y＝ax²+bx来表示，已知OA＝8米，距离O点2米处的棚高BC为 $\frac{9}{4}$ 米.

(1)、求该抛物线的解析式；

(2)、若借助横梁DE（DE∥OA）建一个门，要求门的高度为1.5米，求横梁DE的长度是多少米？

查看试题解析
20. 某小区业主委员会决定把一块长50m，宽30m的矩形空地建成健身广场，设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的矩形），空白区域为活动区，且四周的4个出口宽度相同，其宽度不小于14m，不大于26m，设绿化区较长边为xm，活动区的面积为ym²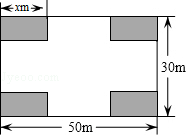

(1)、直接写出：①用x的式子表示出口的宽度为；
②y与x的函数关系式及x的取值范围；

(2)、求活动区的面积y的最大面积；

(3)、预计活动区造价为50元/m² ，绿化区造价为40元/m² ，如果业主委员会投资不得超过72000元来参与建造，当x为整数时，共有几种建造方案？

查看试题解析
21. 已知，在△ABC中，∠ACB＝30°

(1)、如图1，当AB＝AC＝2，求BC的值；

(2)、如图2，当AB＝AC，点P是△ABC内一点，且PA＝2，PB＝ $\sqrt{21}$ ，PC＝3，求∠APC的度数；

(3)、如图3，当AC＝4，AB＝ $\sqrt{7}$ （CB＞CA），点P是△ABC内一动点，则PA+PB+PC的最小值为.

查看试题解析
22. 如图，直线y＝ $\frac{1}{2}$ x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣ $\frac{1}{2}$ x²+bx+c经过A、B两点，与x轴的另一个交点为 C．

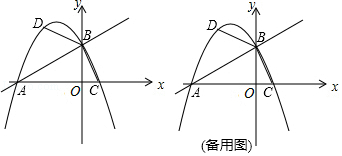(1)、求抛物线的解析式；

(2)、直线AB上方抛物线上的点D，使得∠DBA＝2∠BAC，求D点的坐标；

(3)、M是平面内一点，将△BOC绕点M逆时针旋转90°后，得到△B₁O₁C₁ ，若△B₁O₁C₁的两个顶点恰好落在抛物线上，请求点B₁的坐标．

查看试题解析