湖北省武汉市汉阳区2019届九年级上学期数学期中考试试卷
试卷更新日期:2019-10-09 类型:期中考试
一、单选题
-
1. 一元二次方程 的二次项系数、一次项系数、常系数分别是( )A、3,6,1 B、3,6,-1 C、3,-6,1 D、3,-6,-12. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、3. 下列手机手势解锁图案中,是中心对称图形的是( )A、
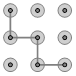 B、
B、 C、
C、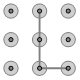 D、
D、 4. 已知x1 , x2是一元二次方程x2﹣6x﹣5=0的两个根,则x1+x2的值是( )A、6 B、﹣6 C、5 D、﹣55. 如图, 的直径为10,弦 , 是 上一个动点,则 的最小值为( )
4. 已知x1 , x2是一元二次方程x2﹣6x﹣5=0的两个根,则x1+x2的值是( )A、6 B、﹣6 C、5 D、﹣55. 如图, 的直径为10,弦 , 是 上一个动点,则 的最小值为( ) A、2 B、3 C、4 D、56. 肥城市刘台“桃花节”观赏人数逐年增加,据有关部门统计,2015年约为20万人次,预计到2017年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )A、20(1+2x)=28.8 B、28.8(1+x)2=20 C、20(1+x)2=28.8 D、20+20(1+x)+20(1+x)2=28.87. 如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( )
A、2 B、3 C、4 D、56. 肥城市刘台“桃花节”观赏人数逐年增加,据有关部门统计,2015年约为20万人次,预计到2017年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )A、20(1+2x)=28.8 B、28.8(1+x)2=20 C、20(1+x)2=28.8 D、20+20(1+x)+20(1+x)2=28.87. 如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( ) A、42° B、48° C、52° D、58°8. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A、42° B、48° C、52° D、58°8. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )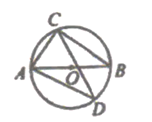 A、35° B、45° C、55° D、65°9. 在抛物线y= ﹣2ax﹣3a上有A(﹣0.5, )、B(2, )和C(3, )三点,若抛物线与y轴的交点在正半轴上,则 、 和 的大小关系为( )A、 < < B、 < < C、 < < D、 < <10. 某学习小组在研究函数 的图象和性质时,已列表、描点并画出了图象的一部分,则方程 实数根的个数为( )
A、35° B、45° C、55° D、65°9. 在抛物线y= ﹣2ax﹣3a上有A(﹣0.5, )、B(2, )和C(3, )三点,若抛物线与y轴的交点在正半轴上,则 、 和 的大小关系为( )A、 < < B、 < < C、 < < D、 < <10. 某学习小组在研究函数 的图象和性质时,已列表、描点并画出了图象的一部分,则方程 实数根的个数为( )…
0
1
2
3
3.5
4
…
…
0
…
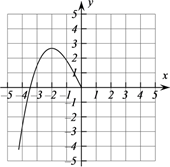 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 一元二次方程 的解是 .12. 某中学组织初三学生篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有个班级参赛.13. 把抛物线y= x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是14. 飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数关系式是s=60t﹣1.5t2 . 飞机着陆后滑行米飞机才能停下来.15. 如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧 上一点,则∠APB的度数为 .
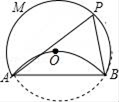 16. 如图, 的半径是1, 为 的弦,将弦 绕点 逆时针旋转 ,得到 ,连 ,则 的最大值为 .
16. 如图, 的半径是1, 为 的弦,将弦 绕点 逆时针旋转 ,得到 ,连 ,则 的最大值为 .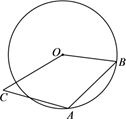
三、解答题
-
17. 解方程18. 二次函数 的图象如图所示,根据图象解答下列问题:
 (1)、直接写出方程 的根;(2)、直接写出不等式 的解集.19. 关于x的一元二次方程x2+(2m﹣1)x+m2=0有实数根.(1)、求m的取值范围;(2)、若两根为x1、x2且x12+x22=7,求m的值.20. 如图, 是等边三角形.
(1)、直接写出方程 的根;(2)、直接写出不等式 的解集.19. 关于x的一元二次方程x2+(2m﹣1)x+m2=0有实数根.(1)、求m的取值范围;(2)、若两根为x1、x2且x12+x22=7,求m的值.20. 如图, 是等边三角形.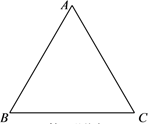 (1)、作 的外接圆;(2)、在劣弧 上取点 ,分别连接 ,并将 绕 点逆时针旋转 ;(3)、若 ,直接写出四边形 的面积.21. 如图, 为 的直径,且 , 为 上一点, 平分 交 于点 , , 于 , 为半圆弧 的中点, 交 于点 .
(1)、作 的外接圆;(2)、在劣弧 上取点 ,分别连接 ,并将 绕 点逆时针旋转 ;(3)、若 ,直接写出四边形 的面积.21. 如图, 为 的直径,且 , 为 上一点, 平分 交 于点 , , 于 , 为半圆弧 的中点, 交 于点 . (1)、求 的长;(2)、求 的长.22. 如图,在足够大的空地上有一段长为 米的旧墙 ,某人利用旧墙和100米长的木栏围成一个矩形菜园 .
(1)、求 的长;(2)、求 的长.22. 如图,在足够大的空地上有一段长为 米的旧墙 ,某人利用旧墙和100米长的木栏围成一个矩形菜园 . (1)、如图1,已知矩形菜园的一边靠墙,且 ,设 米.
(1)、如图1,已知矩形菜园的一边靠墙,且 ,设 米.①若 ,所围成的矩形菜园的面积为450平方米,求所利用旧墙 的长;
②求矩形菜园 面积的最大值;
(2)、如图2,若 ,则旧墙和木栏能围成的矩形菜园 面积的最大值是米2.23. 如图,在等腰 中, ,点 是 内一点,连接 ,且 ,设 .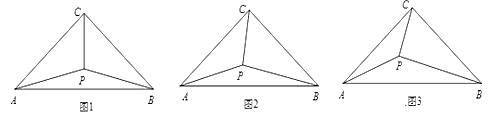 (1)、如图1,若 ,将 绕点 顺时针旋转 至 ,连结 ,易证 为等边三角形,则 , ;(2)、如图2,若 ,则 , ;(3)、如图3,试猜想 和 之间的数量关系,并给予证明.24. 在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)、如图1,若 ,将 绕点 顺时针旋转 至 ,连结 ,易证 为等边三角形,则 , ;(2)、如图2,若 ,则 , ;(3)、如图3,试猜想 和 之间的数量关系,并给予证明.24. 在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.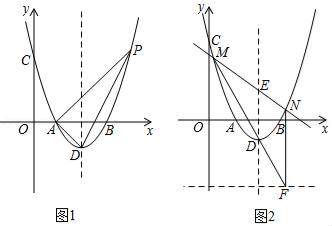 (1)、求此抛物线解析式;(2)、如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;(3)、在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
(1)、求此抛物线解析式;(2)、如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;(3)、在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.