湖北省十堰市丹江口市2019届九年级上学期数学期中考试试卷
试卷更新日期：2019-10-09 类型：期中考试
一、单选题
-
1. 二次函数y=x2﹣2x+2的顶点坐标是（ ）A、（1，1） B、（2，2） C、（1，2） D、（1，3）2. 平面直角坐标系内与点P（﹣2，3）关于原点对称的点的坐标是（ ）A、（3，﹣2） B、（2，3） C、（2，﹣3） D、（﹣3，﹣3）3. 已知抛物线C的解析式为y＝ax2+bx+c，则下列说法中错误的是（ ）A、a确定抛物线的开口方向与大小 B、若将抛物线C沿y轴平移，则a，b的值不变 C、若将抛物线C沿x轴平移，则a的值不变 D、若将抛物线C沿直线l：y＝x+2平移，则a、b、c的值全变4. 如图，B，C是⊙O上两点，且∠α＝96°，A是⊙O上一个动点（不与B，C重合），则∠A为（ ）
A、48° B、132° C、48°或132° D、96°5. 如图，△ABC中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则⊙C的半径为（ ）
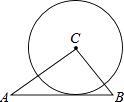A、2.3 B、2.4 C、2.5 D、2.66. 如图.将半径为6cm的圆形纸片折叠后，圆弧恰好经过圆心O.则折痕AB的长为（ ）
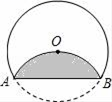A、6cm B、3 cm C、6 cm D、6 cm7. 若二次函数y=mx2﹣4x+m有最大值﹣3，则m等于（ ）A、m=4 B、m=﹣1 C、m=1 D、m=﹣48. 在平面直角坐标系中，将点P（﹣3，2）绕点A（0，1）顺时针旋转90°，所得到的对应点P′的坐标为（ ）A、（﹣1，﹣2） B、（3，﹣2） C、（1，3） D、（1，4）9. 如图，在△ABC中，∠ACB＝90°，AC＝BC＝ ，将△ACB绕点A逆时针旋转60°得到△AC′B′，则CB′的长为（ ）
A、 + B、1+ C、3 D、 +10. 如图，已知二次函数y＝ax2+bx+c的图象经过点（0，3），（x1 ， 0），其中，2＜x1＜3，对称轴为x＝1，则下列结论：①2a﹣b＝0； ②x（ax+b）≤a+b；③方程ax2+bx+c﹣3＝0的两根为x1'＝0，x2'＝2；④﹣3＜a＜﹣1.其中正确的是（ ）
A、②③④ B、①②③ C、②④ D、②③二、填空题
-
11. 已知二次函数y＝ax2+4ax+c的图象与x轴的一个交点为（﹣1，0），则它与x轴的另一个交点的坐标是.12.
抛物线的部分图象如图所示，则当y＜0时，x的取值范围是 ．
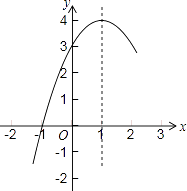13. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连结AA′，若∠1＝20°，则∠B＝度.
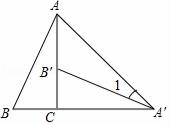14. 如图，C是⊙O的弦BA延长线上一点，已知∠COB＝130°，∠C＝20°，OB＝2，则AB的长为.
15. 如图，正方形ABCD的边长为4cm，以正方形的一边BC为直径在正方形ABCD内作半圆，再过点A作半圆的切线，与半圆切于点F，与CD交于点E，则S梯形ABCE＝cm2.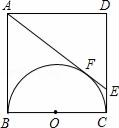
16. 如图，△ABC中，∠C＝90°，AC＝8，BC＝6，E，F分别在边AC，BC，若以EF为直径作圆经过AB上某点D，则EF长的取值范围为.
三、解答题
-
17. 已知抛物线的顶点坐标是（﹣1，﹣4），与y轴的交点是（0，﹣3），求这个二次函数的解析式.18. △ABC与点O在10×10的网格中的位置如图所示
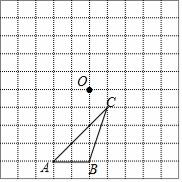(1)、画出△ABC绕点O逆时针旋转90°后的图形；(2)、若⊙M能盖住△ABC，则⊙M的半径最小值为.19. 河上有一座桥孔为抛物线形的拱桥（如图1），水面宽6m时，水面离桥孔顶部3m，因降暴雨水面上升1m.
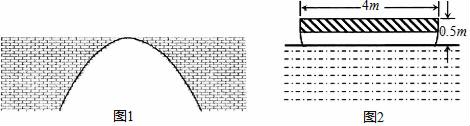(1)、建立适当的坐标系，并求暴雨后水面的宽；(2)、一艘装满物资的小船，露出水面部分高为0.5m、宽4m（横断面如图2所示），暴雨后这艘船能从这座拱桥下通过吗？（注：结果保留根号.）
20. 已知y关于x二次函数y＝x2﹣（2k+1）x+（k2+5k+9）与x轴有交点.(1)、求k的取值范围；(2)、若x1 ， x2是关于x的方程x2﹣（2k+1）x+（k2+5k+9）＝0的两个实数根，且x12+x22＝39，求k的值.21. 如图，台风中心位于点A，并沿东北方向AC移动，已知台风移动的速度为50千米/时，受影响区域的半径为130千米，B市位于点A的北偏东75°方向上，距离A点240千米处.
(1)、说明本次台风会影响B市；(2)、求这次台风影响B市的时间.22. 某宾馆有50个房间供游客居住，当每个房间定价120元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间定价为x元（x为整数）.(1)、直接写出每天游客居住的房间数量y与x的函数解析式.(2)、设宾馆每天的利润为W元，当每间房价定价为多少元时，宾馆每天所获利润最大，最大利润是多少？23. 如图，⊙O是△ABC的外接圆，AB为直径，D是⊙O上一点，且弧CB=弧CD，CE⊥DA交DA的延长线于点E.
(1)、求证：∠CAB＝∠CAE；(2)、求证：CE是⊙O的切线；(3)、若AE＝1，BD＝4，求⊙O的半径长.24. 如图1，已知△ABC中，∠ACB＝90°，CA＝CB，点D，E分别在CB，CA上，且CD＝CE，连AD，BE，F为AD的中点，连CF.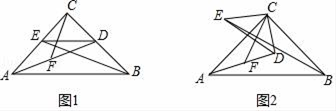
(1)、求证：CF＝ BE，且CF⊥BE；(2)、将△CDE绕点C顺时针旋转一个锐角（如图2），其它条件不变，此时（1）中的结论是否仍成立？并证明你的结论.25. 如图1，抛物线y＝ax2+bx+c的图象与x轴交于A（﹣3，0）、B（1，0）两点，与y轴交于点C，且OC＝OA.
(1)、求抛物线解析式；(2)、过直线AC上方的抛物线上一点M作y轴的平行线，与直线AC交于点N.已知M点的横坐标为m，试用含m的式子表示MN的长及△ACM的面积S，并求当MN的长最大时S的值；(3)、如图2，D（0，﹣2），连接BD，将△OBD绕平面内的某点（记为P）逆时针旋转180°得到△O′B′D′，O、B、D的对应点分别为O′、B′、D′.若点B′、D′两点恰好落在抛物线上，求旋转中心点P的坐标.