湖北省黄石市2019届九年级上学期数学期中考试试卷
试卷更新日期:2019-10-09 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 要使方程 是关于 . 的一元二次方程,则( )A、 B、 C、 且 D、 且 且3. 如果将抛物线 向下平移1个单位,那么所得新抛物线的表达式是( )
2. 要使方程 是关于 . 的一元二次方程,则( )A、 B、 C、 且 D、 且 且3. 如果将抛物线 向下平移1个单位,那么所得新抛物线的表达式是( )
A、 B、 C、 D、4. 若方程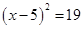 的两根为
的两根为  和
和  ,且 ,则下列结论中正确的是 ( ) A、
,且 ,则下列结论中正确的是 ( ) A、 是19的算术平方根
B、
是19的算术平方根
B、 是19的平方根
C、
是19的平方根
C、 是19的算术平方根
D、
是19的算术平方根
D、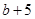 是19的平方根
5. 若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m-1的图象不经过第( )象限.A、四 B、三 C、二 D、一6. 下面对于二次三项式﹣x2+4x﹣5的值的判断正确的是( )A、恒大于0 B、恒小于0 C、不小于0 D、可能为07. 当a>0,b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是( )A、
是19的平方根
5. 若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m-1的图象不经过第( )象限.A、四 B、三 C、二 D、一6. 下面对于二次三项式﹣x2+4x﹣5的值的判断正确的是( )A、恒大于0 B、恒小于0 C、不小于0 D、可能为07. 当a>0,b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是( )A、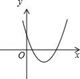 B、
B、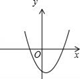 C、
C、 D、
D、 8. 如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )
8. 如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( ) A、4 B、 C、5 D、9. 抛物线y=x2﹣mx﹣m2+1的图象过原点,则m为( )A、0 B、1 C、﹣1 D、±110. 如图1,在△ABC中,AB=BC,AC=m,D,E分别是AB,BC边的中点,点P为AC边上的一个动点,连接PD,PB,PE.设AP=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是( )
A、4 B、 C、5 D、9. 抛物线y=x2﹣mx﹣m2+1的图象过原点,则m为( )A、0 B、1 C、﹣1 D、±110. 如图1,在△ABC中,AB=BC,AC=m,D,E分别是AB,BC边的中点,点P为AC边上的一个动点,连接PD,PB,PE.设AP=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是( ) A、PD B、PB C、PE D、PC
A、PD B、PB C、PE D、PC二、填空题
-
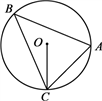
11. 函数y=2(x+1)2+1,当x时,y随x的增大而减小.12. 已知关于x的方程x2+3x+k2=0的一个根是-1,则k=13. 如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为.
 14. 一种药品原价每盒25元,两次降价后每盒16元.设两次降价的百分率都为x,可列方程.15. 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1=.
14. 一种药品原价每盒25元,两次降价后每盒16元.设两次降价的百分率都为x,可列方程.15. 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1=.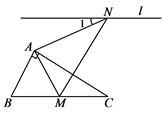 16. 已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为.
16. 已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为. 17. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,求线段OE的长.
17. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,求线段OE的长.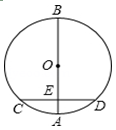
三、解答题
-
18. 解下列一元二次方程.(1)、x2-8x+1=0;(2)、2x2+1=3x.19. 元旦了,九(2)班每个同学都与全班同学交换一件自制的小礼物,结果全班交换小礼物共1560件,求九(2)班有多少个同学?20. 已知抛物线的顶点为(4,﹣8),并且经过点(6,﹣4),试确定此抛物线的解析式.并写出对称轴方程.21. 已知关于x的一元二次方程x2+(2m+1)x+m2−2=0.(1)、若该方程有两个实数根,求m的最小整数值;(2)、若方程的两个实数根为x1 , x2 , 且 ,求m的值.22. 如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
 (1)、三角尺旋转了度。(2)、连接CD,试判断△CBD的形状;(3)、求∠BDC的度数。23. 某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.(1)、写出y与x之间的函数关系式和自变量x的取值范围;(2)、超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?24. 如图
(1)、三角尺旋转了度。(2)、连接CD,试判断△CBD的形状;(3)、求∠BDC的度数。23. 某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.(1)、写出y与x之间的函数关系式和自变量x的取值范围;(2)、超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?24. 如图

 (1)、如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段.(2)、在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.(3)、如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD= ,求BC的长.25. 如图,抛物线
(1)、如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段.(2)、在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.(3)、如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD= ,求BC的长.25. 如图,抛物线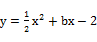 与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
与x轴交于A、B两点,与y轴交于C点,且A(一1,0). 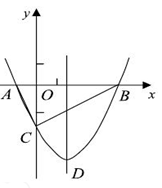 (1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
(1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.