河南省南阳市镇平县2019届九年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{5}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\frac{1}{\sqrt{2}}$

查看试题解析
2. 把方程（x- $\sqrt{5}$ ）(x+ $\sqrt{5}$ ）+(2x-1)²=0化为一元二次方程的一般形式是( )

A、5x²-4x-4=0 B、x²-5=0 C、5x²-2x+1=0 D、5x²-4x+6=0

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $3 \sqrt{5} - \sqrt{5} = 3$ D、 $3 + 2 \sqrt{2} = 5 \sqrt{2}$

查看试题解析
4. 如图，在△ABC中，EF∥BC， $\frac{A E}{E B}$ = $\frac{1}{2}$ ，S_{四边形BCFE}=8，则S_△ABC=（）

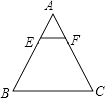A、9 B、10 C、12 D、13

查看试题解析
5. 方程x²－2x－3＝0经过配方法化为(x＋a)²＝b的形式，正确的是（）

A、 ${(x - 1)}^{2} = 4$ B、 ${(x + 1)}^{2} = 4$ C、 ${(x - 1)}^{2} = 16$ D、 ${(x + 1)}^{2} = 16$

查看试题解析
6. 下列方程中，没有实数根的方程是（）

A、 $x^{2} - 12 x + 27 = 0$ B、 $2 x^{2} - 3 x + 2 = 0$ C、 $2 x^{2} + 34 x - 1 = 0$ D、 $x^{2} - 3 x - k^{2} = 0$ （ $k$ 为任意实数）

查看试题解析
7. 如图，以点O为位似中心，将△ABC放大得到△DEF，若AD＝OA，则△ABC与△DEF 的面积之比为（）

A、1：2 B、1：4 C、1：5 D、1：6

查看试题解析
8. 某药品经过两次降价，每瓶零售价由168元降为128元．已知两次降价的百分率相同，每次降价的百分率为x，根据题意列方程得（）

A、168（1+x）²=128 B、168（1﹣x）²=128 C、168（1﹣2x）=128 D、168（1﹣x²）=128

查看试题解析
9. 如图1，在Rt△ABC中，∠ACB=90°，点P以每秒1cm的速度从点A出发，沿折线AC﹣CB运动，到点B停止，过点P作PD⊥AB，垂足为D，PD的长y（cm）与点P的运动时间x（秒）的函数图象如图2所示，当点P运动5秒时，PD的长是（）

A、2cm B、1.8cm C、1.5cm D、1.2cm

查看试题解析
10. 如图，在平面直角坐标系xOy中，点A₁ ， A₂ ， A₃ ， …和B₁ ， B₂ ， B₃ ， …分别在直线y= $\frac{1}{5}$ x+ $\frac{4}{5}$ 和x轴上，△OA₁B₁ ， △B₁A₂B₂ ， △B₂A₃B₃ ， …都是等腰直角三角形，如果A₁（1，1），A₂（ $\frac{7}{2}$ ， $\frac{3}{2}$ ），那么点A₃的纵坐标是（）

A、 $\frac{3}{2}$ B、2cm C、 $\frac{5}{2}$ D、 $\frac{9}{4}$

查看试题解析

二、填空题

11. 在 $\sqrt{8}, \sqrt{12}, \sqrt{18}, \sqrt{20}$ 中，与 $\sqrt{2}$ 是同类二次根式的是.

查看试题解析
12. 一元二次方程x（x﹣7）=0的解是.

查看试题解析
13. 如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的P点处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为米.

查看试题解析
14. 如图，已知△ABC中，AB=8，BC=7，AC=6，E是AB的中点，F是AC边上一个动点.将△AEF沿EF折叠，使点A落在A′处，如果△AEF与原△ABC相似，则EF的长为.

查看试题解析
15. 如图，某小区有一块长为30m ，宽为24m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为480m² ，两块绿地之间及周边有宽度相等的人行通道，则人行通道的宽度为m.

查看试题解析

三、解答题

16. 计算：（ $\sqrt{2}$ ﹣ $\sqrt{3}$ ）²+（2 $\sqrt{3}$ + $\sqrt{6}$ ）×（2 $\sqrt{3}$ ﹣ $\sqrt{6}$ ）.

查看试题解析
17. 先化简，再求值：（x﹣1﹣ $\frac{3}{x + 1}$ ）÷ $\frac{x^{2} + 4 x + 4}{x + 1}$ ，其中x是方程x²+x=0解.

查看试题解析
18.

(1)、解方程x²﹣2x﹣2=0.

(2)、用配方法解方程x²﹣4x+1=0.

查看试题解析
19. 如图，已知直线l₁、l₂、l₃分别截直线l₄于点A、B、C，截直线l₅于点D、E、F，且l₁∥l₂∥l₃.

(1)、如果AB=4，BC=8，EF=12，求DE的长.

(2)、如果DE：EF=2：3，AB=6，求AC的长.

查看试题解析
20. 当m为何值时，关于x的一元二次方程x²﹣4x+m﹣ $\frac{1}{2}$ =0有两个相等的实数根？此时这两个实数根是多少？

查看试题解析
21. 为满足市场需求，新生活超市在端午节前夕购进价格为3元/个的某品牌粽子，根据市场预测，该品牌粽子每个售价4元时，每天能出售500个，并且售价每上涨0.1元，其销售量将减少10个，为了维护消费者利益，物价部门规定，该品牌粽子售价不能超过进价的200%，请你利用所学知识帮助超市给该品牌粽子定价，使超市每天的销售利润为800元．

查看试题解析
22. 正方形ABCD的边长为4，M，N分别是BC，CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直.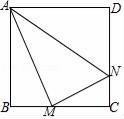

(1)、证明：△ABM∽△MCN；

(2)、若△ABM的周长与△MCN周长之比是4：3，求NC的长.

查看试题解析
23. 如图

如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE. 将△EDC绕点C按顺时针方向旋转，记旋转角为α.

(1)、问题发现
① 当 $α = 0^{\circ}$ 时， $\frac{A E}{B D}$ ；② 当 $α = 180^{\circ}$ 时， $\frac{A E}{B D}$

(2)、拓展探究
试判断：当0°≤α＜360°时， $\frac{A E}{D B}$ 的大小有无变化？请仅就图2的情况给出证明.

(3)、问题解决
当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长.

查看试题解析