河南省南阳市新野县2019届九年级上学期数学期中考试试卷
试卷更新日期:2019-10-09 类型:期中考试
一、单选题
-
1. 方程3x(x-2)=x-2的根为( )A、 B、 C、 , D、2. 下列二次根式中,与 不是同类二次根式的是( )A、 B、 C、 D、3. 关于x的方程ax2﹣3x+1=2x2是一元二次方程,则a的取值范围为( )A、a≠0 B、a>0 C、a≠2 D、a>24. 计算:(4 ﹣3 )÷2 的结果是( )A、2﹣ B、1﹣ C、 D、5. 已知关于x的一元二次方程 有两个相等的实根,则k的值为( )A、 B、 C、2或3 D、 或6. 如图,下列条件不能判定△ADB∽△ABC的是( )
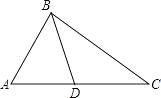 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =7. 如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =7. 如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.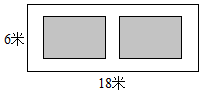 A、2 B、1 C、8或1 D、88.
A、2 B、1 C、8或1 D、88.下列四个三角形中,与图中的三角形相似的是( )
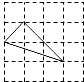 A、
A、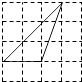 B、
B、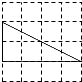 C、
C、 D、
D、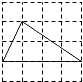 9. 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )
9. 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( ) A、 B、 C、 或 D、 或10. 关于 x 的方程mx2+x﹣m+1=0,有以下三个结论:①当 m=0 时,方程只有一个实数解;②当 m≠0 时,方程有两个不相等的实数解;③无论 m 取何值, 方程都有一个负数解,其中正确的是( )A、①② B、②③ C、①③ D、①②③
A、 B、 C、 或 D、 或10. 关于 x 的方程mx2+x﹣m+1=0,有以下三个结论:①当 m=0 时,方程只有一个实数解;②当 m≠0 时,方程有两个不相等的实数解;③无论 m 取何值, 方程都有一个负数解,其中正确的是( )A、①② B、②③ C、①③ D、①②③二、填空题
-
11. 方程x2-4x=0的解为 .12. 关于x的一元二次方程(k-1)x2+6x+k2-k=0的一个根是0,则k的值是.13. 如图,四边形ABCD中,AD∥BC,∠B=∠ACD=90°,BC=2,DA=3,则△ABC与△DCA的面积比为.
 14. 已知一次函数y=kx+b的大致图象,则关于x的一元二次方程x2-2x+kb+1=0的根的情况是.
14. 已知一次函数y=kx+b的大致图象,则关于x的一元二次方程x2-2x+kb+1=0的根的情况是. 15. 如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.5m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1m,又测得地面的影长为1.5m,请你帮她算一下,树高为.
15. 如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.5m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1m,又测得地面的影长为1.5m,请你帮她算一下,树高为. 16. 小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?
16. 小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?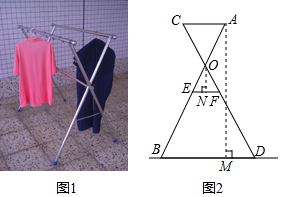
三、解答题
-
17. - ÷ × -( + )23( - )2218.(1)、解方程:(2)、用配方法解方程:3x2=4x+219. 某商店连续一至四月销售额的增长率都相同,今年2月份的销售额是2万元,4月份的销售额是2.88万元.该商店销售额每月的增长率是多少?1月份的销售额是多少?20. 如图,已知ED∥BC,∠EAB=∠BCF.求证:
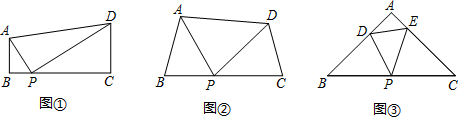
 (1)、四边形ABCD为平行四边形;(2)、OB2=OE•OF;21. 已知:关于x的方程x2-(k+2)x+2k=0(1)、求证:无论k取任何实数值,方程总有实数根;(2)、若等腰三角形ABC的一边长a=1,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.22. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
(1)、四边形ABCD为平行四边形;(2)、OB2=OE•OF;21. 已知:关于x的方程x2-(k+2)x+2k=0(1)、求证:无论k取任何实数值,方程总有实数根;(2)、若等腰三角形ABC的一边长a=1,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.22. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,则DE的长为.
 23. 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的横坐标是一元二次方程x2+2x-3=0的两根(AO>OC),直线AB与y轴交于D,D点的坐标为
23. 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的横坐标是一元二次方程x2+2x-3=0的两根(AO>OC),直线AB与y轴交于D,D点的坐标为 (1)、求直线AB的函数表达式;(2)、在x轴上找一点E,连接EB,使得以点A、E、B为顶点的三角形与△ABC相似(不包括全等),并求点E的坐标;(3)、在(2)的条件下,点P、Q分别是AB和AE上的动点,连接PQ,点P、Q分别从A、E同时出发,以每秒1个单位长度的速度运动,当点P到达点B时,两点停止运动,设运动时间为t秒,问几秒时以点A、P、Q为顶点的三角形与△AEB相似.
(1)、求直线AB的函数表达式;(2)、在x轴上找一点E,连接EB,使得以点A、E、B为顶点的三角形与△ABC相似(不包括全等),并求点E的坐标;(3)、在(2)的条件下,点P、Q分别是AB和AE上的动点,连接PQ,点P、Q分别从A、E同时出发,以每秒1个单位长度的速度运动,当点P到达点B时,两点停止运动,设运动时间为t秒,问几秒时以点A、P、Q为顶点的三角形与△AEB相似.