河南省南阳市西峡县2019届九年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\frac{\sqrt{3 - x}}{x}$ 中x的取值范围是（）

A、x＞3 B、x≤3且x≠0 C、x≤3 D、x＜3且x≠0

查看试题解析
2. 下列二次根式是最简二次根式的是（　　）

A、 $\sqrt{0.1}$ B、 $\sqrt{19}$ C、 $\sqrt{8}$ D、 $\sqrt{4 \frac{1}{4}}$

查看试题解析
3. 一元二次方程x²﹣2x=0的根是（　　）

A、x=2 B、x=0 C、x₁=0，x₂=2 D、x₁=0，x₂=﹣2

查看试题解析
4. 如图，AD∥BE∥CF，直线l₁、l₂与这三条平行线分别交于点A，B，C和点D，E，F.若AB＝4.5，BC＝3，EF＝2，则DE的长度是（）

A、 $\frac{4}{3}$ B、3 C、5 D、 $\frac{27}{4}$

查看试题解析
5. 关于 $x$ 的一元二次方程 $x^{2} + 2 (m - 1) x + m^{2} = 0$ 的根的情况是（）

A、无法确定 B、有两个不等实根 C、有两相等实根 D、有实根

查看试题解析
6. 如图，四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形，若OA：OA'＝2：3，则四边形ABCD与A'B'C'D'的面积比是（）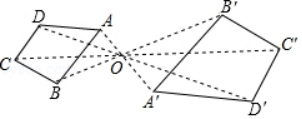

A、4：9 B、2：5 C、2：3 D、 $\sqrt{2}$ ： $\sqrt{3}$

查看试题解析
7. 在Rt△ABC中，∠C＝90°，AB＝4，BC＝3，则cosB等于（）

A、 $\frac{\sqrt{7}}{4}$ B、 $\frac{\sqrt{7}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{3}{4}$

查看试题解析
8. 如图，点D，E分别在△ABC的AB，AC边上，增加下列条件中的一个：①∠AED＝∠B，②∠ADE＝∠C，③ $\frac{A E}{A B} = \frac{D E}{B C}$ ，④ $\frac{A D}{A C} = \frac{A E}{A B}$ ，⑤AC²＝AD•AE，使△ADE与△ACB一定相似的有（）

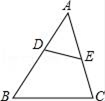A、①②④ B、②④⑤ C、①②③④ D、①②③⑤

查看试题解析
9. 如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m².若设道路的宽为xm，则下面所列方程正确的是（）

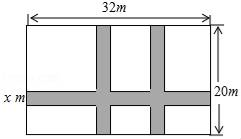A、32x+2×20x＝32×20﹣570 B、（32﹣2x）（20﹣x）＝570 C、（32﹣x）（20﹣x）＝32×20﹣570 D、32x+2×20x﹣2x²＝570

查看试题解析
10. 如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的顶点B的坐标为（）

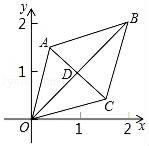A、（0，-2 $\sqrt{2}$ ） B、（2 $\sqrt{2}$ ，0） C、（2，﹣2） D、（﹣2，﹣2）

查看试题解析

二、填空题

11. 计算： $\frac{\sqrt{20} - 1}{\sqrt{5}}$ ＝.

查看试题解析
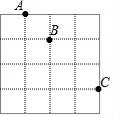
12. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{1}{3}$ ，则 $\frac{2 a + 2 c}{b + d}$ ＝.

查看试题解析
13. 若关于x的一元二次方程ax²+2x﹣1＝0无解，则a的最大整数值是.

查看试题解析
14. 如图在正方形网格中，若A（1，1），B（2，0），则C点的坐标为.

查看试题解析
15. 在Rt△ABC中，BC＝3，AC＝4，点D，E是线段AB，AC上的两个动点（不与A，B，C重合）沿DE翻折△ADE使得点A的对应点F恰好落在直线BC上，当DF与Rt△ABC的一条边垂直的时候，线段AD的长为.

查看试题解析

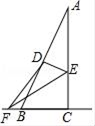
三、解答题

16. 计算：

(1)、 $3 \sqrt{45} \div \sqrt{\frac{1}{5}} \times \frac{2}{3} \sqrt{2 \frac{2}{3}}$ ；

(2)、 $\sqrt{27} - 2 \cos 30^{\circ} - {(\frac{1}{\sqrt{3}})}^{- 1} + {(1 - \sqrt{3})}^{0}$ .

查看试题解析
17. 按要求解下列方程：

(1)、x（x﹣2）+x﹣2＝0（因式分解法）

(2)、2x²﹣3x+1＝0（配方法）

查看试题解析
18. 已知关于x的方程x²+mx+m﹣3＝0.

(1)、若该方程的一个根为2，求m的值及方程的另一个根；

(2)、求证：不论m取何实数，该方程都有两个不相等的实数根.

查看试题解析
19. 如图，在△ABC中，∠C＝90°，点D是边AB上的动点，过点D作DE∥BC交AC于E，过E作EF∥AB交BC于F，连结DF.

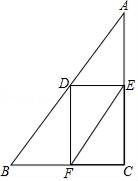(1)、若点D是AB的中点，证明：四边形DFEA是平行四边形；

(2)、若AC＝8，BC＝6，直接写出当△DEF为直角三角形时AD的长.

查看试题解析
20. 如图，四边形ABCD中，AC平分∠DAB，AC²＝AB•AD，∠ADC＝90°，E为AB的中点.

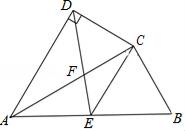(1)、求证：△ADC∽△ACB；

(2)、CE与AD有怎样的位置关系？试说明理由；

(3)、若AD＝4，AB＝6，求 $\frac{A C}{A F}$ 的值.

查看试题解析
21. 某商业街有店面房共100间，2015年平均每间店面房的年租金为1万元，由于物价上涨，到2017年平均每间店面房的年租金上涨到了1.21万元，据预测，当每间的年租金定为12100元时，可全部租出；若每间的年租金每增加0.1万元，就要少租出10间，该商业街管委会要为租出的商铺每间每年交各种费用0.1万元，未租出的商铺每间每年交各种费用0.05万元.

(1)、求2015年至2017年平均每间店面房年租金的平均增长率；

(2)、当每间店面房的年租金上涨多少万元时，该商业街的年收益（收益＝租金﹣各种费用）为103.8万元？

查看试题解析
22. 如图

(1)、观察发现：如图1，在Rt△ABC中，∠B＝90°，点D在边AB上，过D作DE∥BC交AC于E，AB＝5，AD＝3，AE＝4．填空：
①△ABC与△ADE是否相似？（直接回答）；

②AC＝；DE＝．

(2)、拓展探究：将△ADE绕顶点A旋转到图2所示的位置，猜想△ADB与△AEC是否相似？若不相似，说明理由；若相似，请证明．

(3)、迁移应用：将△ADE绕顶点A旋转到点B、D、E在同一条直线上时，直接写出线段BE的长．

查看试题解析
23. 如图1，一次函数y＝ $\frac{1}{2}$ x+4与x轴、y轴分别交于A，B两点．P是x轴上的动点，设点P的横坐标为n．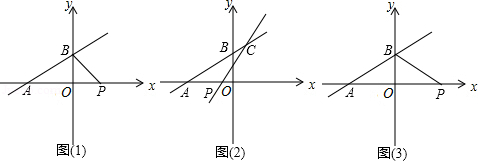

(1)、当△BPO∽△ABO时，求点P的坐标；

(2)、如图2，过点P的直线y＝2x+b与直线AB相交于C，求当△PAC的面积为20时，点P的坐标；

(3)、如图3，直接写出当以A，B，P为顶点的三角形为等腰三角形时，点P的坐标．

查看试题解析