河南省南阳市邓州市2019届九年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，一定是二次根式的是（）

A、 $\sqrt{- 7}$ B、 $\sqrt[3]{m}$ C、 $\sqrt{1 + x^{2}}$ D、 $\sqrt{2 x}$

查看试题解析
2. 下列方程是一元二次方程的是（）

A、x²=﹣1 B、 $x^{2} + \frac{1}{x} = 1$ C、x²+y+1=0 D、x³﹣2x²=1

查看试题解析
3. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，已知AE＝6， $\frac{A D}{A B} = \frac{3}{7}$ ，则EC的长是（）

A、4.5 B、8 C、10.5 D、14

查看试题解析
4. 若 $\sqrt{- a b} = \sqrt{a} \cdot \sqrt{- b}$ 成立，则（）

A、a≥0，b≥0 B、a≥0，b≤0 C、ab≥0 D、ab≤0

查看试题解析
5. 下面是小刚同学在一次测试中解答的部分填空题，其中解答正确的个数是（）
①已知实数a，b满足a= $\sqrt{b - 3} + \sqrt{3 - b}$ +3，即 $\sqrt{a b}$ =3；②若x²=9，则x=3；③有一个角为100°的两个等腰三角形一定相似

A、1 B、2 C、3 D、0

查看试题解析
6. 如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（）

A、 B、 C、 D、

查看试题解析
7. 二次三项式 $x^{2} - 4 x + 3$ 配方的结果是（）

A、 ${(x - 2)}^{2} + 7$ B、 ${(x - 2)}^{2} - 1$ C、 ${(x + 2)}^{2} + 7$ D、 ${(x + 2)}^{2} - 1$

查看试题解析
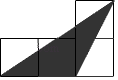8. 某校进行体操队列训练，原有8行10列，后增加40人，使得队伍增加的行数、列数相同，你知道增加了多少行或多少列吗？设增加了 $x$ 行或列，则列方程得（）

A、(8﹣ $x$ ) (10﹣ $x$ )=8×10﹣40 B、(8﹣ $x$ )(10﹣ $x$ )=8×10+40 C、(8+ $x$ )(10+ $x$ )=8×10﹣40 D、(8+ $x$ )(10+ $x$ )=8×10+40

查看试题解析
9. 如图所示，AB=AC，∠A=36°，AB的中垂线交AC于D，则下列结论：①∠C=72°；②BD平分∠ABC；③△ABD是等腰三角形；④△CBD∽△CAB.正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 路边有一根电线杆AB和一块正方形广告牌，有一天，小明突然发现在太阳光照射下，电线杆顶端A的影子刚好落在正方形广告牌B的上边中点G处，而正方形广告牌的影子刚好落在地面上E点（如图），已知BC=5米，正方形边长为3米，DE=4米，则此时电线杆的高度约是（）

A、8米 B、7米 C、6米 D、7.9米

查看试题解析

二、填空题

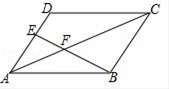
11. 若代数式 $\frac{\sqrt{m + 1}}{m - 1}$ 有意义，则m的取值范围是.

查看试题解析
12. 已知等腰三角形的两边长恰好是方程x²﹣9x+18=0的解，则此等腰三角形的三边长是.

查看试题解析
13. 已知a，b，c为常数，点P（a，c）在第二象限，则关于x的方程ax²+bx+c=0根的情况是.

查看试题解析
14. 如图，在▱ABCD中，E为AD的三等分点，AE= $\frac{2}{3}$ AD，连结BE，交AC于点F，AC=15，则AF为.

查看试题解析
15. 将三角形纸片(△ABC)按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF.已知AB＝AC＝3，BC＝4，若以点B′、F、C为顶点的三角形与△ABC相似，那么BF的长度是.

查看试题解析

三、解答题

16. 先化简，再求值：
$\frac{a^{2} - 2 a b + b^{2}}{2 a - 2 b} \div (\frac{1}{b} - \frac{1}{a})$ ，其中a=2 $\sqrt{\frac{10}{3}}$ ，b=﹣5 $\sqrt{\frac{45}{2}}$ .

查看试题解析
17. 计算或解方程：

(1)、 $\sqrt{18} - \sqrt{\frac{9}{2}} - \frac{\sqrt{3} + \sqrt{6}}{\sqrt{3}} + {(\sqrt{3} - \sqrt{2})}^{0} + \sqrt{{(1 - \sqrt{2})}^{2}}$ .

(2)、2（t+1）²﹣t=1.

(3)、1﹣x=3x²（用配方法解）.

查看试题解析
18. 如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）.

①画出△ABC关于x对称的△A₁B₁C₁；

②以原点O为位似中心，在x轴的上方画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2，并求出△A₂B₂C₂的面积.

查看试题解析
19. 已知关于x的方程x²﹣（2k+1）x+4（k﹣ $\frac{1}{2}$ ）=0

(1)、求证：无论k取何值，这个方程总有实数根；

(2)、若等腰三角形ABC的一边长a=4，另两边b、c恰好是这个方程的两个根，求△ABC的周长．

查看试题解析
20. 如图，在△ABC中，AB=8，BC=16，点P从点A开始沿AB向点B以2m/s的速度移动，点Q从点B开始沿BC向点C以4m/s的速度移动，如果P，Q分别从AB，BC同时出发，经过几秒△PBQ与△ABC相似？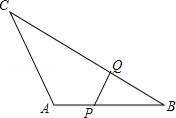

查看试题解析
21. 山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：

(1)、每千克核桃应降价多少元？

(2)、在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？

查看试题解析
22. 如图，矩形ABCD中，AB＝20，BC＝10，点P为AB边上一动点，DP交AC于点Q.

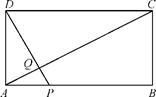(1)、求证：△APQ∽△CDQ；

(2)、P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动，移动时间为t秒.当t为何值时，DP⊥AC?

查看试题解析
23. 如图，在Rt△ABC中，∠ACB＝90°， $\frac{BC}{AC} = \frac{m}{n}$ ，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F.

(1)、探究发现：
如图1，若m＝n，点E在线段AC上，则 $\frac{D E}{D F}$ ＝；

(2)、数学思考：
①如图2，若点E在线段AC上，则 $\frac{D E}{D F}$ ＝（用含m，n的代数式表示）；

②当点E在直线AC上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；

(3)、拓展应用：若AC＝ $\sqrt{5}$ ，BC＝2 $\sqrt{5}$ ，DF＝4 $\sqrt{2}$ ，请直接写出CE的长.

查看试题解析