河南省洛阳市智学大联考2019届九年级上学期数学期中考试试卷
试卷更新日期:2019-10-09 类型:期中考试
一、单选题
-
1. 方程x(x-5)=0化成一般形式后,它的常数项是( )A、 B、5 C、0 D、12. 下面四个手机应用图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如果方程(m-3)x2-(m+3)x+3=0是关于x的一元二次方程,那么m不能取的值为( )A、 B、3 C、 D、都不对4. 二次函数图象上部分点的坐标对应值列表如下:
3. 如果方程(m-3)x2-(m+3)x+3=0是关于x的一元二次方程,那么m不能取的值为( )A、 B、3 C、 D、都不对4. 二次函数图象上部分点的坐标对应值列表如下:x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则该函数图象的对称轴是( )
A、直线x=﹣3 B、直线x=﹣2 C、直线x=﹣1 D、直线x=05. 有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )A、 B、 C、 D、6. 若关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有解,那么m的取值范围是( )A、 B、 C、 且 D、 且7. 下列命题中是真命题的有( )①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的两个圆是等圆;⑤直径是圆中最长的弦.
A、5个 B、4个 C、3个 D、2个8. 如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是46°,则∠ACD的度数为( ) A、46° B、23° C、44° D、67°9. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣310. 如图,垂直于x轴的直线AB分别与抛物线 : (x≥0)和抛物线 : (x≥0) 交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则 的值为( )
A、46° B、23° C、44° D、67°9. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣310. 如图,垂直于x轴的直线AB分别与抛物线 : (x≥0)和抛物线 : (x≥0) 交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则 的值为( )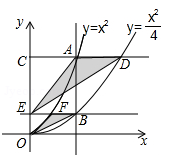 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若关于x的一元二次方程ax2+bx+6=0的一个根为x=2,则代数式2a+b+6的值为.12. 已知抛物线y=x2-(k+2)x+9的顶点在坐标轴上,则k的值是.13. 两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=cm.
 14. 如图,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,①abc<0,②2a+b>0,③a-b+c<0,④b2>4ac,⑤关于x的方程ax2+bx+c-2=0没有实数根.则下列结论正确的有.(填序号)
14. 如图,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,①abc<0,②2a+b>0,③a-b+c<0,④b2>4ac,⑤关于x的方程ax2+bx+c-2=0没有实数根.则下列结论正确的有.(填序号) 15. 如图,△ ABC 中,∠BAC=90°,AB=3,AC=4,点 D 是 BC 的中点,将△ ABD 沿 AD 翻折得到△ AED,连 CE,则线段 CE 的长等于
15. 如图,△ ABC 中,∠BAC=90°,AB=3,AC=4,点 D 是 BC 的中点,将△ ABD 沿 AD 翻折得到△ AED,连 CE,则线段 CE 的长等于
三、解答题
-
16. 先化简,再求值:( - )÷ - +x,其中x满足方程x2-5x+2=017. 在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
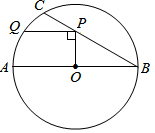 (1)、如图当PQ∥AB时,求PQ的长;(2)、当点P在BC上移动时,线段PQ长的最大值为;此时,∠POQ的度数为.18. 为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)、如图当PQ∥AB时,求PQ的长;(2)、当点P在BC上移动时,线段PQ长的最大值为;此时,∠POQ的度数为.18. 为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2. (1)、求y与x之间的函数关系式,并注明自变量x的取值范围;(2)、请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?19. 已知△ABC在平面直角坐标系中的位置如图所示.
(1)、求y与x之间的函数关系式,并注明自变量x的取值范围;(2)、请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?19. 已知△ABC在平面直角坐标系中的位置如图所示. (1)、写出A,B,C三点的坐标;(2)、将△ABC绕着点C顺时针方向旋转90°后得到△A1B2C,画出旋转后的△A1B1C,并写出A1 , B1的坐标.20. 已知二次函数的图象经过最高点(2,5)和点(0,4).(1)、试确定此二次函数的解析式;(2)、请你用图象法判断方程 的根的情况.(画出简图)21. 已知关于x的一元二次方程-x2+(3-k)x+k-1=0,其中k为常数.(1)、求证:无论k为何值,方程总有两个不相等的实数根;(2)、若函数y=-x2+(3-k)x+k-1的图象不经过第二象限,求k的取值范围.22. 两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.
(1)、写出A,B,C三点的坐标;(2)、将△ABC绕着点C顺时针方向旋转90°后得到△A1B2C,画出旋转后的△A1B1C,并写出A1 , B1的坐标.20. 已知二次函数的图象经过最高点(2,5)和点(0,4).(1)、试确定此二次函数的解析式;(2)、请你用图象法判断方程 的根的情况.(画出简图)21. 已知关于x的一元二次方程-x2+(3-k)x+k-1=0,其中k为常数.(1)、求证:无论k为何值,方程总有两个不相等的实数根;(2)、若函数y=-x2+(3-k)x+k-1的图象不经过第二象限,求k的取值范围.22. 两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点. (1)、如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为和位置关系为;(2)、如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;(3)、如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.23. 如图,抛物线y=ax2+bx+c经过点A(2,﹣3),且与x轴交点坐标为(﹣1,0),(3,0)
(1)、如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为和位置关系为;(2)、如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;(3)、如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.23. 如图,抛物线y=ax2+bx+c经过点A(2,﹣3),且与x轴交点坐标为(﹣1,0),(3,0) (1)、求抛物线的解析式;(2)、在直线AB下方抛物线上找一点D,求出使得△ABD面积最大时点D的坐标;(3)、点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在直线AB下方抛物线上找一点D,求出使得△ABD面积最大时点D的坐标;(3)、点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.