河南省安阳市林州市2019届九年级上学期数学期中考试试卷
试卷更新日期：2019-10-09 类型：期中考试
一、单选题
-
1. 一元二次方程 配方后可化为（ ）A、 B、 C、 D、2. 下列图形中是轴对称图形，而不是中心对称图形的是（ ）A、等腰梯形 B、矩形 C、平行四边形 D、菱形3. 如图，点A，B，C是⊙O上的三点，已知∠AOB＝100°，那么∠ACB的度数是（ ）
A、30° B、40° C、50° D、60°4. 一元二次方程x2﹣x﹣3＝0的根的情况为（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根5. 如图， ， 是 的直径， ，若 ，则 的度数是（ ）
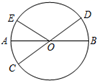A、32° B、60° C、68° D、64°6. 已知⊙O的半径是5，直线l是⊙O的切线，那么点O到直线l的距离是（ ）A、2.5 B、3 C、5 D、107. 已知二次函数y＝ax2+bx+c（a≠0）的图象如图，则下列结论中正确的是（ ）
A、ac＞0 B、当x＞1时，y随x的增大而增大 C、2a+b＝1 D、方程ax2+bx+c＝0有一个根是x＝38. 如图，AB是⊙O的直径，点C，D在⊙O上， ，OD∥AC，下列结论错误的是（ ）
A、∠BOD＝∠BAC B、∠BOD＝∠COD C、∠BAD＝∠CAD D、∠C＝∠D9. 如图，l1与l3交于点P，l2与l3交于点Q，∠1＝104°，∠2＝87°，要使得l1∥l2 ， 下列操作正确的是（ ）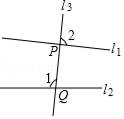
A、将l1绕点P逆时针旋转14° B、将l1绕点P逆时针旋转17° C、将l2绕点Q顺时针旋转11° D、将l2绕点Q顺时针旋转14°二、填空题
-
10. 方程x2﹣3x=0的解是 ．11. 已知x=2是关于x的一元二次方程kx2+（k2﹣2）x+2k+4=0的一个根，则k的值为 ．12. 如图，在矩形ABCD中， AB=3， AD=4，若以点 A为圆心，以 4为半径作 ⊙A，则点 A，点B，点 C，点 D四点中在 ⊙A外的是.
13. 已知△ABC的三边长分别是6，8，10，则△ABC外接圆的直径是.14. 如图，在Rt△ABC中，∠C＝90°，∠B＝40°，点D在边BC上，BD＝2CD，把△ABC绕点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，则m＝.
三、解答题
-
15.(1)、2x2﹣5x﹣1＝0；(2)、6x2﹣3x﹣1＝2x﹣216. 已知：关于x的一元二次方程x2+2x+k=0有两个不相等的实数根．(1)、求k的取值范围；(2)、当k取最大整数值时，用合适的方法求该方程的解．17. 如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(-2，2)，B(0，5)，C(0，2).
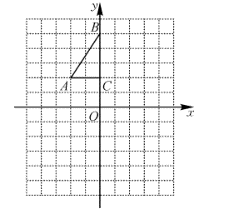
①将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形.
②平移△ABC，使点A的对应点A2坐标为(-2，-6)，请画出平移后对应的△A2B2C2的图形.
③若将△A1B1C绕某一点旋转可得到△A2B2C2 ， 请直接写出旋转中心的坐标.
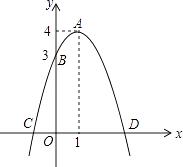
18. 已知二次函数y=﹣x2+2x+m．
(1)、如果二次函数的图象与x轴有两个交点，求m的取值范围；
(2)、如图，二次函数的图象过点A（3，0），与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．
(3)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围．
19. 在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A'B'C.
(1)、如图1，当AB∥CB'时，设A'B'与CB相交于点D，求证：△A'CD是等边三角形.(2)、若E为AC的中点，P为A'B'的中点，则EP的最大值是多少，这时旋转角θ为多少度.20. 如图，在△ABC中，AB=AC，点D在BC上，BD=DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．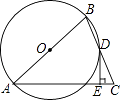
(1)、求证：AB是⊙O的直径；
(2)、判断DE与⊙O的位置关系，并加以证明；
(3)、若⊙O的半径为3，∠BAC=60°，求DE的长．
