湖北省武汉市新洲区阳逻街2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个数：1、－2、0、－3，其中最小的一个是（）

A、1 B、－2 C、0 D、－3

查看试题解析
2. 单项式 $- \frac{1}{3} x y$ 的系数和次数分别是（）

A、 $- \frac{1}{3}$ ，1 B、 $- \frac{1}{3}$ ，2 C、 $\frac{1}{3}$ ，1 D、 $\frac{1}{3}$ ，2

查看试题解析
3. 小明给希望工作捐款15000元，15000用科学记数法表示为（）

A、15×10³ B、1.5×10³ C、1.5×10⁴ D、1.5×10⁵

查看试题解析
4. 下列各数中互为相反数的是（）

A、－5与-|-5| B、+（-8）与-（+8） C、-（-3）与－3 D、-1³与（-1）³

查看试题解析
5. -（m-n）去括号得（）

A、m-n B、-m+n C、-n-m D、m+n

查看试题解析
6. 已知 $2 x^{6} y^{2}$ 和－ $\frac{1}{3} x^{3 m} y^{n}$ 是同类项，则m+n=（）

A、8 B、6 C、4 D、无法确定

查看试题解析
7. 下面计算正确的是（）

A、3x²-x²=3 B、3a²+2a³=5a⁵ C、-0.25ab+ $\frac{1}{4}$ ab=0 D、x+3=3x

查看试题解析
8. 已知|a|=5，|b|=3，且|a-b|=b-a，则a+b的值为（）

A、8 B、8或—2 C、2或—2 D、—2或—8

查看试题解析
9. 点M在数轴上距原点6个单位长度，将M向左移动2个单位长度至N点，点N表示的数是（）

A、4 B、－4 C、8或－4 D、－8或4

查看试题解析
10. 设实数a，b，c满足a＞b＞c(ac＜0)，且|c|＜|b|＜|a|，则|x-a|+|x+b|+|x-c|的最小值为（）

A、 $\frac{| a + b + c |}{3}$ B、|b| C、a+b D、－c－a

查看试题解析

二、填空题

11. 计算：（-1）+2=.

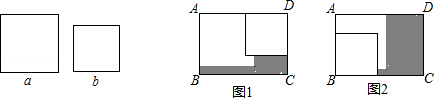
查看试题解析
12. 若一个两位数的十位上的数是a，个位上的数是b，则这个两位数是（用含a，b的式子表示）.

查看试题解析
13. 若多项式2x³－8x²＋x－1与多项式3x³＋2mx²－5x＋3的和不含x的二次项，则m＝.

查看试题解析
14. 已知代数式x+2y的值是3，则代数式2x+4y+1的值是．

查看试题解析
15. 若a与b互为相反数，c与d互为倒数，则2019a+2018b+bcd=.

查看试题解析
16. 在长方形ABCD内，将两张边长分别为a和b（a＞b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S₁ ，图2中阴影部分的面积为S₂ ．当AD﹣AB=2时，S₂﹣S₁的值为．（用a、b的代数式表示）

查看试题解析

三、解答题

17. 计算：

(1)、3－7－﹙－7﹚＋﹙－6﹚；

(2)、－2³×2 $\frac{1}{4}$ ＋﹙－ $\frac{3}{2}$ ﹚²÷﹙－ $\frac{1}{2}$ ﹚³；

查看试题解析
18. 计算：

(1)、﹙3x²＋2x＋1﹚－﹙2x²＋x－1﹚；

(2)、5﹙x²－2y﹚－2﹙x²＋4y﹚；

查看试题解析
19. 先化简，再求值：
3a²＋[a²＋﹙5a²－2a﹚－3﹙a²－3a﹚]，其中a＝－2；

查看试题解析
20. 某检修小组，某天乘一辆汽车检修东西走向的“汉施公路”时，约定向东行驶为正，向西行驶为负，他们从A地出发到收工时的行走记录为（单位：千米）：－4，+7，－9，+8，+6，－5，+10，－8.

(1)、收工时，该小组距离A地多远？

(2)、若汽车行驶每千米耗油0.2升，那么从A地出发到回到A地共耗油多少升？

查看试题解析
21. 有理数a，b，c在数轴上的位置如图所示：

(1)、比较a，|b|，c的大小（用“＜”连接）；

(2)、若m＝|a＋b|－|c－a|－|b－1|，求1－2017(m＋c)²⁰¹⁷的值.

查看试题解析
22. 已知含字母m，n的代数式是： $3 [m^{2} + 2 (n^{2} + m n - 3)] - 3 (m^{2} + 2 n^{2}) - 4 (m n - m - 1)$ .

(1)、化简这个代数式.

(2)、小明取m，n互为倒数的一对数值代入化简的代数式中，恰好计算得代数式的值等于0.那么小明所取的字母n的值等于多少？

(3)、聪明的小智从化简的代数式中发现，只要字母n取一个固定的数，无论字母m取何数，代数式的值恒为一个不变的数，那么小智所取的字母n的值是多少呢？

查看试题解析
23. 把2016个正整数1、2、3、4、……、2016按如图方式排列成一个表，用一方框按如图所示的方式任意框住9个数.（方框只能平移）

(1)、若框住的9个数中，正中间的一个数为39，则：这九个数的和为.

(2)、方框能否框住这样的9个数，它们的和等于2016？若能，请写出这9个数；若不能，请说明理由。

(3)、若任意框住9个数的和记为S，则：S的最大值与最小值之差等于.

查看试题解析
24. 已知点A，B在数轴上表示的数分别为a，b，且|a+6|+(b-18)²=0（规定：数轴上A，B两点之间的距离记为AB）.

(1)、求b-a的值.

(2)、数轴上是否存在点C，使得CA=3CB？若存在，请求出点C所表示的数；若不存在，请说明理由.

(3)、动点P从点A出发，以每秒1个单位长度的速度沿数轴向右匀速运动，动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，且P比Q先运动2秒.问点Q运动多少秒时，P，Q相距4个单位长度？

查看试题解析