湖北省武汉市洪山区2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 温度由﹣4℃上升7℃是（）

A、3℃ B、﹣3℃ C、11℃ D、﹣11℃

查看试题解析
2. 下列各组运算中，运算中结果相同的是（）

A、2³和3² B、（﹣4）³和﹣4³ C、﹣5²和（﹣5）² D、（﹣ $\frac{2}{3}$ ）²和（﹣ $\frac{3}{2}$ ）³

查看试题解析
3. 下列计算正确的是（）

A、3a+2a=5a² B、3a－a=3 C、2a³+3a²=5a⁵ D、－a²b+2a²b=a²b

查看试题解析
4. 武汉长江二桥是世界上第一座弧线形钢塔斜拉桥，该桥全长16800m，用科学记数法表示这个数为（）.

A、1.68×10⁴m B、16.8×10³m C、0.168×10⁴m D、1.68×10³m

查看试题解析
5. 一个多项式加上﹣2a+7等于3a²+a+1，则这个多项式是（）

A、3a²﹣a﹣6 B、3a²+3a+8 C、3a²+3a﹣6 D、﹣3a²﹣3a+6

查看试题解析
6. 将正整数1至2018按一定规律排列如下表：

平移表中带阴影的方框，方框中三个数的和可能是（）

A、2018 B、2019 C、2040 D、2049

查看试题解析
7. 有理数a、b、c在数轴上位置如图，化简|a+c|﹣|a﹣b﹣c|+2|b﹣a|﹣|b﹣c|的值为（）

A、2a﹣2b+3c B、c C、﹣4a+4b﹣c D、﹣2b+c

查看试题解析
8. 把四张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为m厘米，宽为n厘米）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（）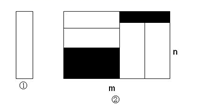

A、4m厘米 B、4n厘米 C、2（m+n）厘米 D、4（m-n）厘米

查看试题解析
9. 某部门组织调运一批物资从A地到B地，一运送物资车从A地出发，出发第一小时内按原计划的60千米/小时匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前20分钟到达目的地.设A地到B地距离为x千米，则根据题意得原计划规定的时间为（）

A、 $\frac{x}{90}$ + $\frac{1}{3}$ B、 $\frac{x}{90} - \frac{1}{3}$ C、 $\frac{x}{90} + \frac{2}{3}$ D、 $\frac{x}{90} + \frac{4}{3}$

查看试题解析
10. 下列去括号或添括号：
①3a²﹣6a﹣4ab+1＝3a²﹣[6a﹣（4ab﹣1）]②2a﹣2（﹣3x+2y﹣1）＝2a+6x﹣4y+2③a²﹣5a﹣ab+3＝（a²﹣ab）﹣（5a+3）④3ab﹣[5ab²﹣（2a²b﹣2）﹣a²b²]＝3ab﹣5ab²+2a²b﹣2+a²b²其中正确的有（）个

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. $- \frac{1}{2}$ 的相反数的倒数是.

查看试题解析
12. 多项式2a²b﹣πab²﹣ab的次数为.

查看试题解析
13. 已知小明的年龄是m岁，小红的年龄比小明的年龄的2倍少4岁，小华的年龄比小红的年龄的 $\frac{1}{2}$ 还多1岁，请用含m的式子表示这三人的年齡和.

查看试题解析
14. 数轴上点M表示有理数﹣3，将点M向右平移2个单位长度到达点N，点E到点N的距离为5，则点E表示的有理数为.

查看试题解析
15. 我们定义三个有理数之间的新运算法则“⊕”：a⊕b⊕c＝ $\frac{1}{2}$ （|a﹣b﹣c|+a+b+c），如：1⊕（﹣2）⊕3＝ $\frac{1}{2}$ [|1﹣（﹣2）﹣3|+1+（﹣2）+3]＝l，在﹣2，﹣4，﹣5，0，2，5，6这7个数中，任意取三个数作为a，b，c的值，进行“a⊕b⊕c“运算，求在所有计算的结果中的最大值是.

查看试题解析
16. 已知数轴上有A、B、C三个点对应的数分别是a、b、c，满足|a+24|+|b+10|+（c﹣10）²=0；动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒.当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A.在返回过程中，当t=秒时，P、Q两点之间的距离为2.

查看试题解析

三、解答题

17. 今年的“十•一”黄金周是7天的长假，某风景区在7天假期中每天旅游人数变化如表（正号表示人数比前一天多，负号表示比前一天少），若9月30日的游客人数为4.2万人.

日期

1日

2日

3日

4日

5日

6日

7日

人数变化

单位：万人

+1.8

﹣0.6

+0.8

﹣0.7

﹣1.3

+0.5

﹣2.4

(1)、10月4日的旅客人数为人；

(2)、在7天假期中，旅客人数最多的一天比最少的一天多人；

(3)、如果每一万人带来的经济收入约为100万元，则黄金周7天的旅游总收入约为多少万元？

查看试题解析

18. 计算或化简

(1)、（﹣6）÷|﹣ $\frac{3}{4}$ |﹣（﹣1）³×（﹣7）

(2)、﹣2³×[（﹣ $\frac{2}{3}$ ）+ $\frac{1}{2}$ ]﹣6×（﹣ $\frac{2}{3}$ ）²÷ $\frac{2}{3}$ ﹣（ $\frac{3}{8} + \frac{1}{6} - \frac{3}{4}$ ）+（﹣ $\frac{1}{24}$ ）

(3)、 $\frac{1}{2}$ x﹣2（x﹣ $\frac{1}{3} y^{2}$ ）+（﹣ $\frac{3}{2} x + \frac{1}{3} y^{2}$ ）

查看试题解析
19. 一辆出租车从超市出发，向东走4千米到达小丽家，然后向西走2千米到达小华家，又向西走6千米达到小敏家，最后回到超市.

(1)、以超市为原点，规定向东为正方向，用1个单位长度表示1千米，你能在数轴上标出小丽家，小华家和小敏家的位置吗？

(2)、出租车一共行驶了多少千米？

查看试题解析
20. 观察下面三行数
﹣2，4，﹣8，16，﹣32，64，…①

0，6，﹣6，18，﹣30，66，…②

5，﹣1，11，﹣13，35，﹣61，……③

(1)、第①行数的第7个数是；

(2)、设第②行数中有一个数为a，第③行数中对应位置的数为b，则a和b之间等量关系为；设第①行数的第n个数为x，取每行的第n个数，这三个数的和是；

(3)、根据（2）中的结论，若取每行的第9个数，计算这三个数的和.

查看试题解析
21. 先化简，再求值.
已知|x﹣3|+（y+ $\frac{2}{3}$ ）²＝0，先化简再求值：3x²y﹣[2xy²﹣3（xy﹣ $\frac{3}{2}$ x²y）+xy]+5xy²

查看试题解析
22. 已知：A=2x²+ax﹣5y+b，B=bx²﹣ $\frac{3}{2}$ x﹣ $\frac{5}{2}$ y﹣3.

(1)、求3A﹣（4A﹣2B）的值；

(2)、当x取任意数值，A﹣2B的值是一个定值时，求（a+ $\frac{3}{14}$ A）﹣（2b+ $\frac{3}{7}$ B）的值.

查看试题解析
23. 用1块A型钢板可制成2块C型钢板和1块D型钢板；用1块B型钢板可制成1块C型钢板和3块D型钢板.现购买A、B型钢板共100块，并全部加工成C、D型钢板.设购买A型钢板x块（x为整数）

(1)、可制成C型钢板块（用含x的代数式表示）；可制成D型钢板块[用含x的代数式表示）.

(2)、出售C型钢板每块利润为100元，D型钢板每块利润为120元.若将C、D型钢板全部出售，通过计算说明此时获得的总利润.

(3)、在（2）的条件下，若20≤x≤25，请你设计购买方案使此时获得的总利润最大，并求出最大的总利润.

查看试题解析
24. 在数轴上，点A表示数a，点B表示数b，在学习绝对值时，我们知道了绝对值的几何含义：
数轴上A、B之间的距离记作|AB|，定义：|AB|＝|a﹣b|.如：|a+6|表示数a和﹣6在数轴上对应的两点之间的距离.|a﹣1|表示数a和1在数轴上对应的两点之间的距离.

(1)、若a满足|a+6|+|a+4|+|a﹣1|的值最小，b与3a互为相反数，直接写出点A对应的数，点B对应的数.

(2)、在（1）的条件下，已知点E从点A出发以1单位/秒的速度向右运动，同时点F从点B出发以2单位/秒的速度向右运动，FO的中点为点P，则下列结论：①PO+AE的值不变；②PO﹣AE的值不变，其中有且只有一个是正确的，选出来并求其值.

(3)、在（1）的条件下，已知动点M从A点出发以1单位/秒的速度向左运动，动点N从B点出发以3单位/秒的速度向左运动，动点T从原点的位置出发以x单位/秒的速度向左运动，三个动点同时出发，若运动过程中正好先后出现两次TM＝TN的情况，且两次间隔的时间为4秒，求满足条件的x的值.

查看试题解析