湖北省鄂州市鄂城区2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2019-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $2 \times (- 3)$ 的结果是（）

A、6 B、－6 C、－1 D、5

查看试题解析
2. 5的相反数是（）

A、 - $\frac{1}{5}$ B、 $\frac{1}{5}$ C、﹣5 D、5

查看试题解析
3. 绝对值等于 $\frac{2}{3}$ 的数与-3 $\frac{1}{2}$ 的和等于（　　）

A、 $\frac{8}{21}$ B、4 $\frac{1}{6}$ C、 $\frac{20}{21}$ 或- $\frac{8}{21}$ D、-2 $\frac{5}{6}$ 或-4 $\frac{1}{6}$

查看试题解析
4. 下列说法正确的个数有（）
①若|a|＝|b|，则a＝b；②若a≠b，则a²≠b²；③若a＞b，则a²＞b²；④a²＞a.

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 下列各式计算正确的是 ( )

A、6a+a=6a² B、-2a+5b=3ab C、4m²n-2mn²=2mn D、3ab²-5b²a=-2ab²

查看试题解析
6. 丁丁做了以下4道计算题：
（ 1 ）（﹣1）²⁰⁰⁴＝2004；（2）0﹣（﹣1）＝1；（3）﹣ $\frac{1}{2} + \frac{1}{3} = - \frac{1}{6}$ ；（4） $\frac{1}{2} \div (- \frac{1}{2}) = - 1$ ；

请你帮他检查一下，他一共做对了（）

A、1题 B、2题 C、3题 D、4题

查看试题解析
7. 有理数a，b在数轴上表示的点如图所示，则a，﹣a，b，﹣b的大小关系是（）

A、﹣b＞a＞﹣a＞b B、a＞﹣a＞b＞﹣b C、b＞a＞﹣b＞﹣a D、﹣b＜a＜﹣a＜b

查看试题解析
8. 下面的说法正确的是（　　）

A、﹣2不是单项式 B、﹣a表示负数 C、 $\frac{3 a b}{5}$ 的系数是3 D、x+ $\frac{a}{x}$ +1不是多项式

查看试题解析
9. 若ab＞0，则 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{a b}{| a b |}$ 的值为（）

A、3 B、﹣1 C、±1或±3 D、3或﹣1

查看试题解析
10. 多项式 $\frac{1}{2}$ x^|m|y﹣（m﹣3）xy+7是关于x、y的四次三项式，则m的值是（）

A、3或﹣3 B、﹣3 C、4或﹣4 D、3

查看试题解析

二、填空题

11. 用“＜”“＞”或“＝”号填空：

(1)、﹣ $\frac{4}{5}$ ﹣ $\frac{3}{4}$ ；

(2)、﹣（﹣0.01）（﹣ $\frac{1}{10}$ ）²；

(3)、3.9950（精确到0.01）3.999.

查看试题解析
12. 我国雾霾天气多发，PM2.5颗粒物被称为大气的元凶.PM2.5是指直径小于或等于2.5微米的颗粒物，已知1毫米=1000微米，用科学记数法表示2.5微米是毫米.

查看试题解析
13. 设a是最小的正整数，b是最大的负整数，c是绝对值最小的有理数，则a﹣b+c＝.

查看试题解析
14. 已知mx²yⁿ^﹣¹+4x²y⁹＝0，（其中x≠0，y≠0）则m+n＝.

查看试题解析
15. 一个多项式A减去多项式2x²+5x﹣3，马虎同学将2x²+5x﹣3抄成了2x²+5x+3，计算结果是﹣x²+3x﹣7，那么这个多项式A是.

查看试题解析
16. 数a，b、c在数轴上的位置如图所示：化简：|a﹣b|﹣|b﹣c|﹣|a|的结果是.

查看试题解析
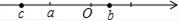17. 在数轴上，点A表示1，点C与点A间的距离为3，则点C所表示的数是.

查看试题解析
18. 如图是由相同的花盆按一定的规律组成的正多边形图案，其中第1个图形一共有6个花盆，第2个图形一共有12个花盆，第3个图形一共有20个花盆，…，则第n个图形中花盆的个数为．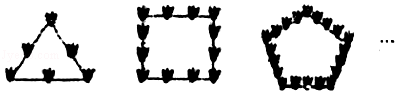

查看试题解析

三、解答题

19. 计算

(1)、（ $\frac{1}{2} - \frac{5}{9} + \frac{5}{6} - \frac{7}{12}$ ）×（﹣36）

(2)、﹣3²+（﹣ $\frac{5}{2}$ ）²×（﹣ $\frac{4}{25}$ ）+|﹣2²|+（﹣1）²⁰¹³；

(3)、36×（﹣99 $\frac{17}{18}$ ）；

(4)、﹣13× $\frac{2}{3}$ ﹣0.34× $\frac{2}{7}$ + $\frac{1}{3}$ ×（﹣13）﹣ $\frac{5}{7}$ ×0.34（用简便方法计算）

查看试题解析
20. 已知a、b互为相反数且a≠0，c、d互为倒数，m的绝对值是最小的正整数，求|m|﹣ $\frac{a}{b} + \frac{2018 (a + b)}{2019}$ ﹣cd的值.

查看试题解析
21. 若|a|＝1，|b|＝2，|c|＝4，且|a+b﹣c|＝a+b﹣c，求a+b+c的值.

查看试题解析
22. 先化简，再求值：（2a²b+2ab²）﹣[2（a²b﹣1）+3ab²+2]，其中a＝2，b＝﹣1.

查看试题解析
23. 已知：A＝ax²+x﹣1，B＝3x²﹣2x+1（a为常数）

(1)、若A与B的和中不含x²项，则a＝；

(2)、在①的基础上化简：B﹣2A.

查看试题解析

24. 有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：

与标准质量的差值（单位：千克）	-3	-2	-1.5	0	1	2.5
筐数	1	4	2	3	2	8

(1)、20筐白菜中，最重的一筐比最轻的一筐重多少千克?

(2)、与标准质量比较，20筐白菜总计超过或不足多少千克?

(3)、若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元?（结果保留整数）

查看试题解析

25. 观察算式：1×3+1＝4＝2²；2×4+1＝9＝3²；3×5+1＝16＝4²；4×6+1＝25＝5² ， …

(1)、请根据你发现的规律填空：6×8+1＝²；

(2)、用含n的等式表示上面的规律：；

(3)、用找到的规律解决下面的问题：
计算：（1+ $\frac{1}{1 \times 3}$ ）（1+ $\frac{1}{2 \times 4}$ ）（1+ $\frac{1}{3 \times 5}$ ）（1+ $\frac{1}{4 \times 6}$ ）…（1+ $\frac{1}{11 \times 33}$ ）

查看试题解析
26. 阅读下面材料并解决有关问题：
我们知道：|x|= ${\begin{matrix} x (x > 0) \\ 0 (x = 0) \\ - x (x < 0) \end{matrix}$ ．现在我们可以用这一结论来化简含有绝对值的代数式，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1=0和x﹣2=0，分别求得x=﹣1，x=2（称﹣1，2分别为|x+1|与|x﹣2|的零点值）．在实数范围内，零点值x=﹣1和，x=2可将全体实数分成不重复且不遗漏的如下3种情况：
①x＜﹣1；②﹣1≤x＜2；③x≥2．
从而化简代数式|x+1|+|x﹣2|可分以下3种情况：
①当x＜﹣1时，原式=﹣（x+1）﹣（x﹣2）=﹣2x+1；
②当﹣1≤x＜2时，原式=x+1﹣（x﹣2）=3；
③当x≥2时，原式=x+1+x﹣2=2x﹣1．综上讨论，原式= ${\begin{matrix} - 2 x + 1 (x < - 1) \\ 3 (- 1 \leq x < 2) \\ 2 x - 1 (x \geq 2) \end{matrix}$ ．
通过以上阅读，请你解决以下问题：

(1)、化简代数式|x+2|+|x﹣4|．

(2)、求|x﹣1|﹣4|x+1|的最大值．

查看试题解析